
De Moivre's formula: a COOL proof
A quick way of proving De Moivre's formula! Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook Hi again everyone, Chris Tisdell here again. In this presentation I am going to continue my series of videos on complex numbers. In particular, in this presentation, I am g
From playlist Intro to Complex Numbers

Math 135 Complex Analysis Lecture 11 022415: Consequences of the Cauchy Integral Formula
Simple calculations using the Cauchy Integral Formula; Cauchy's integral formula for derivatives; Morera's Formula; observation regarding removable singularities; Cauchy's inequality; first Liouville's theorem; Fundamental Theorem of Algebra
From playlist Course 8: Complex Analysis

Euler's formulas, Rodrigues' formula
In this video I proof various generalizations of Euler's formula, including Rodrigues' formula and explain their 3 dimensional readings. Here's the text used in this video: https://gist.github.com/Nikolaj-K/eaaa80861d902a0bbdd7827036c48af5
From playlist Algebra
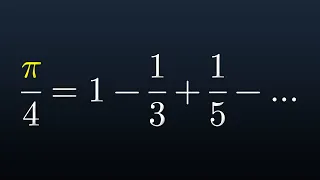
Your New Favorite Formula For Pi
Visit http://brilliant.org/BriTheMathGuy/ to get started learning STEM for free, and the first 200 people will get 20% off their annual premium subscription. This is known as the Leibniz Pi formula. We'll use a whole bunch of series knowledge and even some complex analysis! Let's figure
From playlist Complex Analysis

Colloquium MathAlp 2016 - Vincent Vargas
La théorie conforme des champs de Liouville en dimension 2 La théorie conforme des champs de Liouville fut introduite en 1981 par le physicien Polyakov dans le cadre de sa théorie des sommations sur les surfaces de Riemann. Bien que la théorie de Liouville est très étudiée dans le context
From playlist Colloquiums MathAlp

Pre-Calculus - Using the difference of angles for cosine to evaluate for an angle cos(225-30)
👉 Learn how to evaluate the cosine of an angle in radians using the sum/difference formulas. To do this, we first express the given angle as a sum or a difference of two (easy to evaluate) angles, then we use the unit circle and the Pythagoras theorem to identify the angles and obtain all
From playlist Sum and Difference Formulas

Norbert Verdier : When He was one hundred Years old!
In this Talks we will don’t speak about Joseph-Louis Lagrange (1736-1813) but about Lagrange’s reception at the nineteenth Century. “Who read Lagrange at this Times?”, “Why and How?”, “What does it mean being a mathematician or doing mathematics at this Century” are some of the questions o
From playlist Lagrange Days at CIRM

2021's Biggest Breakthroughs in Math and Computer Science
It was a big year. Researchers found a way to idealize deep neural networks using kernel machines—an important step toward opening these black boxes. There were major developments toward an answer about the nature of infinity. And a mathematician finally managed to model quantum gravity. R
From playlist Discoveries
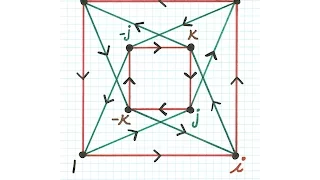
Euler's Formula for the Quaternions
In this video, we will derive Euler's formula using a quaternion power, instead of a complex power, which will allow us to calculate quaternion exponentials such as e^(i+j+k). If you like quaternions, this is a pretty neat formula and a simple generalization of Euler's formula for complex
From playlist Math

Fundamental Theorem of Algebra
In this video, I prove the Fundamental Theorem of Algebra, which says that any polynomial must have at least one complex root. The beauty of this proof is that it doesn’t use any algebra at all, but instead complex analysis, more specifically Liouville’s Theorem. Enjoy!
From playlist Complex Analysis

Guillaume Remy (Columbia) -- Integrability of boundary Liouville CFT
Liouville theory is a fundamental example of a conformal field theory (CFT) first introduced by A. Polyakov in the context of string theory. In recent years it has been rigorously studied using probabilistic techniques. In this talk we will study the integrable structure of Liouville CFT o
From playlist Northeastern Probability Seminar 2020

Trigonometry 7 The Cosine of the Sum and Difference of Two Angles
A geometric proof of the cosine of the sum and difference of two angles identity.
From playlist Trigonometry

Learn where the formula for the Law of Sines comes from
👉 Learn how to solve for the length of the sides and the measures of the angles of a triangle using the law of sines. The law of sines is used in determining the length of the opposite side to a known angle measure or the measure of the opposite angle to a known side length of a triangle.
From playlist Law of Sines | Learn About

Polyhedral Liouville domains - Marco Castronovo
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Polyhedral Liouville domains Speaker: Marco Castronovo Affiliation: Columbia University Date: March 25, 2022 I will explain the construction of a new class of Liouville domains that live in a complex torus o
From playlist Mathematics

Trig identities: De Moivre's formula
How to obtain trig identities from De Moivre's formula. Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook Okay so we are asked to write sin4θ in terms of cosθ and sinθ by applying De Moivre’s Theorem, or De Moivre’s formula, and hence write this product as a functio
From playlist Intro to Complex Numbers

Morris Ang (MIT) -- Integrability of the conformal loop ensemble
For κ between 8/3 and 8, the conformal loop ensemble CLEκ is a canonical random ensemble of loops which is conformally invariant in law, and whose loops locally look like Schramm-Loewner evolution with parameter κ. It describes the scaling limits of the Ising model, percolation, and other
From playlist Northeastern Probability Seminar 2021

Liouville's Theorem through Symplectic Geometry
Liouville's theorem in classical mechanics is almost immediate in its symplectic geometry incarnation. Here I describe why! In the previous video, I introduced Lie derivatives on vector fields, including a derivation that the symplecitc form is preserved under Hamiltonian flow: https://
From playlist Symplectic geometry and mechanics

Liouville's number, the easiest transcendental and its clones (corrected reupload)
This is a corrected re-upload of a video from a couple of weeks ago. The original version contained one too many shortcut that I really should not have taken. Although only two viewers stumbled across this mess-up it really bothered me, and so here is the corrected version of the video, ho
From playlist Recent videos

What is the formula for the law of sines
👉 Learn how to solve for the length of the sides and the measures of the angles of a triangle using the law of sines. The law of sines is used in determining the length of the opposite side to a known angle measure or the measure of the opposite angle to a known side length of a triangle.
From playlist Law of Sines | Learn About

Modular bootstrap, Segal's axioms and resolution of Liouville conformal field theory -Rhodes, Vargas
Mathematical Physics Seminar Topic: Modular bootstrap, Segal's axioms and resolution of Liouville conformal field theory Speakers: Rémi Rhodes; Vincent Vargas Affiliation: Université Aix-Marseille; École Normale Supérieure Date: May 04, 2022 Liouville field theory was introduced by Polya
From playlist Mathematics