
Lie Groups and Lie Algebras: Lesson 18- Group Generators
Lie Groups and Lie Algebras: Lesson 18- Generators This is an important lecture! We work through the calculus of *group generators* and walk step-by-step through the exploitation of analyticity. That is, we use the Taylor expansion of the continuous functions associated with a Lie group o
From playlist Lie Groups and Lie Algebras

Group actions in abstract algebra
In this first video on group actions, I use an example of some previous work on the symmetric group to give you some intuition about group actions. Beware when reading your textbook. It is probably unnecessary difficult just due to the dot notation that is used when describing group acti
From playlist Abstract algebra

Lie groups: Lie groups and Lie algebras
This lecture is part of an online graduate course on Lie groups. We discuss the relation between Lie groups and Lie algebras, and give several examples showing how they behave differently. Lie algebras turn out to correspond more closely to the simply connected Lie groups. We then explain
From playlist Lie groups

This lecture is part of an online graduate course on Lie groups. We define the Lie algebra of a Lie group in two ways, and show that it satisfied the Jacobi identity. The we calculate the Lie algebras of a few Lie groups. For the other lectures in the course see https://www.youtube.co
From playlist Lie groups

In this video I demonstrate an example of a non-faithful group actions, where the identity permutation is actually mapped to by all the elements in the group set. Another example shows you how group actions involving a group set on itself gives rise to group element composition as we see
From playlist Abstract algebra

Lie Groups and Lie Algebras: Lesson 22 - Lie Group Generators
Lie Groups and Lie Algebras: Lesson 22 - Lie Group Generators A Lie group can always be considered as a group of transformations because any group can transform itself! In this lecture we replace the "geometric space" with the Lie group itself to create a new collection of generators. P
From playlist Lie Groups and Lie Algebras
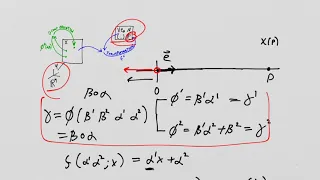
Lie Groups and Lie Algebras: Lesson 16 - representations, connectedness, definition of Lie Group
Lie Groups and Lie Algebras: Lesson 16 - representations, connectedness, definition of Lie Group We cover a few concepts in this lecture: 1) we introduce the idea of a matrix representation using our super-simple example of a continuous group, 2) we discuss "connectedness" and explain tha
From playlist Lie Groups and Lie Algebras

Abstract Algebra: Group actions are defined as a formal mechanism that describes symmetries of a set X. A given group action defines an equivalence relation, which in turn yields a partition of X into orbits. Orbits are also described as cosets of the group. U.Reddit course materials a
From playlist Abstract Algebra

Lie groups: Positive characteristic is weird
This lecture is part of an online graduate course on Lie groups. We give several examples to show that, over fields of positive characteristic, Lie algebras can behave strangely, and have a weaker connection to Lie groups. In particular the Lie algebra does not generate the ring of all in
From playlist Lie groups

Askold Khovanskii: Complex torus, its good compactifications and the ring of conditions
Abstract: Let X be an algebraic subvariety in (ℂ∗)n. According to the good compactifification theorem there is a complete toric variety M⊃(ℂ∗)n such that the closure of X in M does not intersect orbits in M of codimension bigger than dimℂX. All proofs of this theorem I met in literature ar
From playlist Algebraic and Complex Geometry

Ana Balibanu: The partial compactification of the universal centralizer
Abstract: Let G be a semisimple algebraic group of adjoint type. The universal centralizer is the family of centralizers in G of regular elements in Lie(G), parametrized by their conjugacy classes. It has a natural symplectic structure, obtained by Hamiltonian reduction from the cotangent
From playlist Algebra
Is the variety of singular tuples of matrices a null cone? - Viswambhara Makam
Computer Science/Discrete Mathematics Seminar II Topic: Is the variety of singular tuples of matrices a null cone? - Speaker: Viswambhara Makam Affiliation: Member, School of Mathematics Date: February 25, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Jean Michel BISMUT - Fokker-Planck Operators and the Center of the Enveloping Algebra
The heat equation method in index theory gives an explicit local formula for the index of a Dirac operator. Its Lagrangian counterpart involves supersymmetric path integrals. Similar methods can be developed to give a geometric formula for semi simple orbital integrals associated with the
From playlist Integrability, Anomalies and Quantum Field Theory

Moduli of p-divisible groups (Lecture 4) by Ehud De Shalit
PROGRAM PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France
From playlist Perfectoid Spaces 2019

David Zywina, Computing Sato-Tate and monodromy groups.
VaNTAGe seminar on May 5, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Lie Groups for Deep Learning w/ Graph Neural Networks
Lie Groups encode the symmetry of systems. We examine actions of a Lie group on a vector space, given their algebraic, topological and analysis based connectome. Deep Learning algorithms for Graph Neural Networks (GNN) are non trivial, and to understand them Lie Groups are essential! A r
From playlist Learn Graph Neural Networks: code, examples and theory

An introduction to Invariant Theory - Harm Derksen
Optimization, Complexity and Invariant Theory Topic: An introduction to Invariant Theory Speaker: Harm Derksen Affiliation: University of Michigan Date: June 4, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Lie groups: Poincare-Birkhoff-Witt theorem
This lecture is part of an online graduate course on Lie groups. We state the Poincare-Birkhoff Witt theorem, which shows that the universal enveloping algebra (UEA) of a Lie algebra is the same size as a polynomial algebra. We prove it for Lie algebras of Lie groups and sketch a proof of
From playlist Lie groups

This lecture is part of an online graduate course on Lie groups. We give an introductory survey of Lie groups theory by describing some examples of Lie groups in low dimensions. Some recommended books: Lie algebras and Lie groups by Serre (anything by Serre is well worth reading) Repre
From playlist Lie groups

Macro Activity- The FEDexes Fix the the Economy
This is an awesome activity that will help you apply what you are learning in your macroeconomics class. Specifically, monetray policy and the role of the Federal Reserve. Teachers: I made a video that gives you more details about how to run this activity and gives you the link to the the
From playlist Clifford's Favorite Videos