
Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra

Camillo De Lellis: Ill-posedness for Leray solutions of the ipodissipative Navier-Stokes equations
Abstract: In a joint work with Maria Colombo and Luigi De Rosa we consider the Cauchy problem for the ipodissipative Navier-Stokes equations, where the classical Laplacian −Δ is substited by a fractional Laplacian (−Δ)α. Although a classical Hopf approach via a Galerkin approximation shows
From playlist Partial Differential Equations

In this video, I prove the famous Riemann-Lebesgue lemma, which states that the Fourier transform of an integrable function must go to 0 as |z| goes to infinity. This is one of the results where the proof is more important than the theorem, because it's a very classical Lebesgue integral
From playlist Real Analysis

Burnside's Lemma (Part 2) - combining math, science and music
Part 1 (previous video): https://youtu.be/6kfbotHL0fs Orbit-stabilizer theorem: https://youtu.be/BfgMdi0OkPU Burnside's lemma is an interesting result in group theory that helps us count things with symmetries considered, e.g. in some situations, we don't want to count things that can be
From playlist Traditional topics, explained in a new way

Measure Theory 3.1 : Lebesgue Integral
In this video, I define the Lebesgue Integral, and give an intuition for such a definition. I also introduce indicator functions, simple functions, and measurable functions.
From playlist Measure Theory

Chapter 3: Lagrange's theorem, Subgroups and Cosets | Essence of Group Theory
Lagrange's theorem is another very important theorem in group theory, and is very intuitive once you see it the right way, like what is presented here. This video also discusses the idea of subgroups and cosets, which are crucial in the development of the Lagrange's theorem. Other than c
From playlist Essence of Group Theory
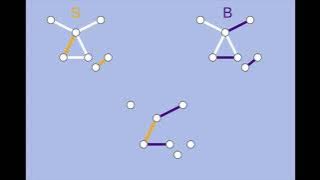
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

Measure Theory 2.1 : Lebesgue Outer Measure
In this video, I introduce the Lebesgue outer measure, and prove that it is, in fact, an outer measure. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Measure Theory

Mathematics of Turbulent Flows: A Million Dollar Problem! by Edriss S Titi
URL: https://www.icts.res.in/lecture/1/details/1661/ Turbulence is a classical physical phenomenon that has been a great challenge to mathematicians, physicists, engineers and computational scientists. Chaos theory has been developed in the end of the last century to address similar phen
From playlist Public Lectures

We finally get to Lagrange's theorem for finite groups. If this is the first video you see, rather start at https://www.youtube.com/watch?v=F7OgJi6o9po&t=6s In this video I show you how the set that makes up a group can be partitioned by a subgroup and its cosets. I also take a look at
From playlist Abstract algebra

Non-uniqueness of Leray solutions of the forced Navier-Stokes equations - Dallas Albritton
Seminar in Analysis and Geometry Topic: Non-uniqueness of Leray solutions of the forced Navier-Stokes equations Speaker: Dallas Albritton Affiliation: Member, School of Mathematics Date: January 18, 2022
From playlist Mathematics

Non-uniqueness of Leray solutions of the forced Navier-Stokes equations - Maria Colombo
Workshop on Recent developments in incompressible fluid dynamics Topic: Non-uniqueness of Leray solutions of the forced Navier-Stokes equations Speaker: Maria Colombo Affiliation: EPFL Date: April 08, 2022 In his seminal work, Leray demonstrated the existence of global weak solutions, wi
From playlist Mathematics

Ladyzhenskaya Lecture 2022 | Mimi Dai - A path of understanding fluid equations
Mimi Dai (University of Illinois, Chicago) A path of understanding fluid equations: from Leray to Ladyzhenskaya, and beyond The mathematical theory of incompressible fluids, Ladyzhenskaya’s favorite topic, still poses challenges for us today. We briefly review the pioneering work of Leray
From playlist Various Lectures
Wild Weak Solutions to Equations arising in Hydrodynamics - 1/6 - Vlad Vicol
In this course, we will discuss the use of convex integration to construct wild weak solutions in the context of the Euler and Navier-Stokes equations. In particular, we will outline the resolution of Onsager's conjecture as well as the recent proof of non-uniqueness of weak solutions to t
From playlist Hadamard Lectures 2020 - Vlad Vicol and - Wild Weak Solutions to Equations arising in Hydrodynamics

Wild Weak Solutions to Equations arising in Hydrodynamics - 3/6 - Vlad Vicol
In this course, we will discuss the use of convex integration to construct wild weak solutions in the context of the Euler and Navier-Stokes equations. In particular, we will outline the resolution of Onsager's conjecture as well as the recent proof of non-uniqueness of weak solutions to t
From playlist Hadamard Lectures 2020 - Vlad Vicol and - Wild Weak Solutions to Equations arising in Hydrodynamics

Wild Weak Solutions to Equations arising in Hydrodynamics - 2/6 - Vlad Vicol
In this course, we will discuss the use of convex integration to construct wild weak solutions in the context of the Euler and Navier-Stokes equations. In particular, we will outline the resolution of Onsager's conjecture as well as the recent proof of non-uniqueness of weak solutions to t
From playlist Hadamard Lectures 2020 - Vlad Vicol and - Wild Weak Solutions to Equations arising in Hydrodynamics

Lorenzo Brandolese: Geometric structures in 2D Navier-Stokes flows
Geometric structures naturally appear in fluid motions. One of the best known examples is Saturn’s Hexagon, the huge cloud pattern at the level of Saturn’s north pole, remarkable both for the regularity of its shape and its stability during the past decades. In this paper we will address t
From playlist Jean-Morlet Chair - Hieber/Monniaux

Intermittency, Cascades and Thin Sets in Three-Dimensional Navier-Stokes Turbulenc by John D. Gibbon
Program Turbulence: Problems at the Interface of Mathematics and Physics (ONLINE) ORGANIZERS: Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (Indian Institute of Science, Bengaluru) DATE: 07 December 202
From playlist Turbulence: Problems at The Interface of Mathematics and Physics (Online)

In this video, I present an overview (without proofs) of the Lebesgue integral, which is a more general way of integrating a function. If you'd like to see proods of the statements, I recommend you look at fematika's channel, where he gives a more detailed look of the Lebesgue integral. In
From playlist Real Analysis