
Determine the Volume of a Rectangular Prism (Whole Numbers)
This video explains how to determine the volume of a rectangular prism. http://mathispower4u.com
From playlist Volume and Surface Area (Geometry)

Adding Whole Numbers and Applications 4
U01_L2_T1_we4 Adding Whole Numbers and Applications 3
From playlist Developmental Math

Calculus 1 Lecture 0.2 Part 7: Introduction to Functions.
From playlist Calculus 1 Playlist 1

Multiplying Monomials and Polynomials 7
In this video, we present a worked example to review basic factoring of quadratic expressions
From playlist Exponents

#48. Rectangular Room is 6 feet Longer than Twice it's Width and Perimeter is 180. Find Dimensions.
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys #48. Rectangular Room is 6 feet Longer than Twice it's Width and Perimeter is 180. Find Dimensions.
From playlist College Algebra Final Exam Review

Commutative algebra 24 Artinian modules
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We define Artinian rings and modules, and give several examples of them. We then study finite length modules, show that they
From playlist Commutative algebra

The Bernstein Sato polynomial: Holonomic modules
This is the third of three talks about the Bernstein-Sato polynomial. The first talk is at https://youtu.be/CX2iej9NKzs We use Bernstein's inequality from the second talk to show that holonomic modules have finite length. We then use this to prove that a particular module is holonomic, wh
From playlist Commutative algebra

What is the Span of a Set of Vectors?
What is the Span of a Set of Vectors? Definition of the span of a set of vectors.
From playlist Linear Algebra

Arc length of vector functions example
Free ebook http://tinyurl.com/EngMathYT Example of how to calculate arc length of a vector function.
From playlist A second course in university calculus.

UXSS 2016 - Dr. Agostino Marinelli
Dr. Agostino Marinelli from SLAC National Accelerator Laboratory presents "Introduction to the Physics of Free Electron Lasers" on June 13, 2016 at the Ultrafast X-ray Summer Seminar, hosted by Stanford PULSE Institute at SLAC National Accelerator Laboratory.
From playlist Stanford PULSE Institute
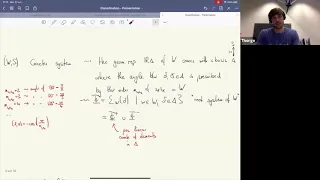
Simple Modules for SL2 via BN-Pairs - Lars Thorge Jensen
Seminar on SL2 Topic: Simple Modules for SL2 via BN-Pairs Speaker: Lars Thorge Jensen Affiliation: Member, School of Mathematics Date: October 27, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Variables Defined & Writing Algebraic Expressions
I define Mathematical Quantities and explain the difference between constant and variable quantities. Variables, Algebraic Expressions, and Numerical Expressions are also defined before working through many examples of writing algebraic expressions from phrases or sentences. I include Ad
From playlist Algebra 1

Repeating decimals and congruences
In this video we give an example on how congruences can be used to compute the length of a decimal expansion. The content of this video corresponds to Section 8.0 of my book "Number Theory and Geometry" which you can find here: https://alozano.clas.uconn.edu/number-theory-and-geometry/
From playlist Number Theory and Geometry

Modular Forms | Modular Forms; Section 1 2
We define modular forms, and borrow an idea from representation theory to construct some examples. My Twitter: https://twitter.com/KristapsBalodi3 Fourier Theory (0:00) Definition of Modular Forms (8:02) In Search of Modularity (11:38) The Eisenstein Series (18:25)
From playlist Modular Forms

[BOURBAKI 2017] 21/10/2017 - 2/4 - Simon RICHE
La théorie de Hodge des bimodules de Soergel [d'après Soergel et Elias-Williamson] ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHenriPoincare/ Twitter : https://twitter.com/In
From playlist BOURBAKI - 2017

The Rust Book (v2) part 39 - Chapter 11 - Testing
I'm streaming every weekday morning on Twitch at https://www.twitch.tv/brookzerker. Please feel free to stop by and say hi! Links Rust book: https://doc.rust-lang.org/book/second-edition/ My code: https://github.com/BrooksPatton/learning-rust The Learning Wiki: https://github.com/BrooksP
From playlist Rust Book

Martina Scolamiero 9/15/21: Extracting persistence features with hierarchical stabilisation
Title: Extracting persistence features with hierarchical stabilisation Abstract: It is often complicated to understand complex correlation patterns between multiple measurements on a dataset. In multi-parameter persistence we represent them through algebraic objects called persistence mo
From playlist AATRN 2021

C. Soulé - Arithmetic Intersection (Part1)
Let X be a 2-dimensional, normal, flat, proper scheme over the integers. Assume ¯L and ¯M are two hermitian line bundles over X. Arakelov (and Deligne) defined a real number ¯L.¯M, the arithmetic intersection number of ¯L and ¯M. We shall explain the definition and the basic properties of
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

1.4.4 Length of a vector (Now also visit http://www.ulaff.net)
1.4.4 Length of a vector
From playlist LAFF - Week 1

In this video we introduce Fermat's little theorem and give a proof using congruences. The content of this video corresponds to Section 7.2 of my book "Number Theory and Geometry" which you can find here: https://alozano.clas.uconn.edu/number-theory-and-geometry/
From playlist Number Theory and Geometry