
Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra

Dali Shen: Interpreting Lauricella hypergeometric system as a Dunkl system
The lecture was held within the framework of the Hausdorff Trimester Program: Periods in Number Theory, Algebraic Geometry and Physics. Abstract: In the 80's of last century, Deligne and Mostow studied the monodromy problem of Lauricella hypergeometric functions and gave a rigorous treatm
From playlist HIM Lectures: Trimester Program "Periods in Number Theory, Algebraic Geometry and Physics"

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Christian SCHUBERT - New Techniques for Worldline Integration
The worldline formalism provides an alternative to Feynman diagrams in the construction of amplitudes and effective actions that shares some of the superior properties of the organization of amplitudes in string theory. In particular, it allows one to write down integral representations co
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Paul Shafer:Reverse mathematics of Caristi's fixed point theorem and Ekeland's variational principle
The lecture was held within the framework of the Hausdorff Trimester Program: Types, Sets and Constructions. Abstract: Caristi's fixed point theorem is a fixed point theorem for functions that are controlled by continuous functions but are necessarily continuous themselves. Let a 'Caristi
From playlist Workshop: "Proofs and Computation"

Multivariable Calculus | Differentiability
We give the definition of differentiability for a multivariable function and provide a few examples. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus
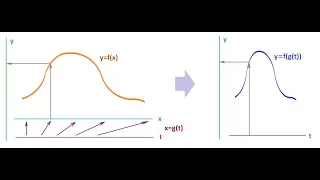
Change of variables and the derivative -- Calculus I
This lecture is on Calculus I. It follows Part I of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus I

Calculus: The Fundamental Theorem of Calculus
This is the second of two videos discussing Section 5.3 from Briggs/Cochran Calculus. In this section, I discuss both parts of the Fundamental Theorem of Calculus. I briefly discuss why the theorem is true, and work through several examples applying the theorem.
From playlist Calculus

The adjoint Brascamp-Lieb inequality - Terence Tao
Analysis and Mathematical Physics Topic: The adjoint Brascamp-Lieb inequality Speaker: Terence Tao Affiliation: University of California, Los Angeles Date: March 08, 2023 The Brascamp-Lieb inequality is a fundamental inequality in analysis, generalizing more classical inequalities such a
From playlist Mathematics

The Field With One Element and The Riemann Hypothesis (Full Video)
A crash course of Deninger's program to prove the Riemann Hypothesis using a cohomological interpretation of the Riemann Zeta Function. You can Deninger talk about this in more detail here: http://swc.math.arizona.edu/dls/ Leave some comments!
From playlist Riemann Hypothesis

Calculus 1 (Stewart) Ep 22, Mean Value Theorem (Oct 28, 2021)
This is a recording of a live class for Math 1171, Calculus 1, an undergraduate course for math majors (and others) at Fairfield University, Fall 2021. The textbook is Stewart. PDF of the written notes, and a list of all episodes is at the class website. Class website: http://cstaecker.f
From playlist Math 1171 (Calculus 1) Fall 2021

Equidistribution of Unipotent Random Walks on Homogeneous spaces by Emmanuel Breuillard
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

What is Green's theorem? Chris Tisdell UNSW
This lecture discusses Green's theorem in the plane. Green's theorem not only gives a relationship between double integrals and line integrals, but it also gives a relationship between "curl" and "circulation". In addition, Gauss' divergence theorem in the plane is also discussed, whic
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Real Analysis Ep 32: The Mean Value Theorem
Episode 32 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class. This episode is more about the mean value theorem and related ideas. Class webpage: http://cstaecker.fairfield.edu/~cstaecker/courses/2020f3371/ Chris Staecker
From playlist Math 3371 (Real analysis) Fall 2020

Pythagorean theorem - What is it?
► My Geometry course: https://www.kristakingmath.com/geometry-course Pythagorean theorem is super important in math. You will probably learn about it for the first time in Algebra, but you will literally use it in Algebra, Geometry, Trigonometry, Precalculus, Calculus, and beyond! That’s
From playlist Geometry

Wolfram Physics Project: Working Session Sept. 15, 2020 [Physicalization of Metamathematics]
This is a Wolfram Physics Project working session on metamathematics and its physicalization in the Wolfram Model. Begins at 10:15 Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the
From playlist Wolfram Physics Project Livestream Archive

Johnathan Bush (7/8/2020): Borsuk–Ulam theorems for maps into higher-dimensional codomains
Title: Borsuk–Ulam theorems for maps into higher-dimensional codomains Abstract: I will describe Borsuk-Ulam theorems for maps of spheres into higher-dimensional codomains. Given a continuous map from a sphere to Euclidean space, we say the map is odd if it respects the standard antipodal
From playlist AATRN 2020

Worldwide Calculus: Extrema and the Mean Value Theorem
Lecture on 'Extrema and the Mean Value Theorem' from 'Worldwide Differential Calculus' and 'Worldwide AP Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Worldwide Single-Variable Calculus for AP®

How to apply the 2nd ftc with secant squared
👉 Learn about the fundamental theorem of calculus. The fundamental theorem of calculus is a theorem that connects the concept of differentiation with the concept of integration. The theorem is basically saying that the differentiation of the integral of a function yields the original funct
From playlist Evaluate Using The Second Fundamental Theorem of Calculus