
How to determine eigenvalues of a boundary value problem
How to determine the eigenvalues of a boundary value problem. A basic Sturm Liouville differential equation is discussed, subject to some boundary conditions. We determine necessary conditions for the problem to admit positive eigenvalues. We also show how to prove the problem has exact
From playlist Differential equations

Moving on from Lagrange's equation, I show you how to derive Hamilton's equation.
From playlist Physics ONE

Lagrange multipliers: 2 constraints
Free ebook http://tinyurl.com/EngMathYT A lecture showing how to apply the method of Lagrange multipliers where two contraints are involved.
From playlist Lagrange multipliers
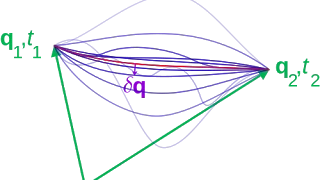
The Beltrami Identity is a necessary condition for the Euler-Lagrange equation (so if it solves the E-L equation, it solves the Beltrami identity). Here it is derived from the total derivative of the integrand (e.g. Lagrangian).
From playlist Physics

Multivariable Calculus | Lagrange multipliers
We give a description of the method of Lagrange multipliers and provide some examples -- including the arithmetic/geometric mean inequality. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus

Lagrange multipliers: 2 constraints
Download the free PDF http://tinyurl.com/EngMathYT This video shows how to apply the method of Lagrange multipliers to a max/min problem. Such ideas are seen in university mathematics.
From playlist Several Variable Calculus / Vector Calculus

(4.1.1): Boundary Value Problems
This video defines a boundary value problems and then provides two examples of solving boundary value problems https://mathispower4u.com
From playlist Differential Equations: Complete Set of Course Videos
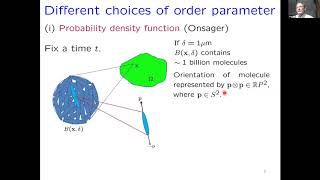
Seminar In the Analysis and Methods of PDE (SIAM PDE): Sir John Ball
The talk will discuss some energy minimization problems for liquid crystals described at different levels of detail by the probability density function of molecular orientations, by a tensor average of this function (the de Gennes Q tensor theory), and by the expected orientation of molecu
From playlist Seminar In the Analysis and Methods of PDE (SIAM PDE)
A Taste of Calculus of Variations
Dirichlet's Principle In this video, I give you a taste of calculus of variations by illustrating Dirichlet's principle, which says that a function u is a minimizer of a certain Dirichlet energy (kinetic + potential energy) if and only if u solves Poisson's equation. This is a neat way of
From playlist Partial Differential Equations

12. Constrained Optimization; Equality Constraints and Lagrange Multipliers
MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015 View the complete course: http://ocw.mit.edu/10-34F15 Instructor: James Swan Students continued to learn how to solve optimization problems that include equality constraints and inequality constraints, as well as the L
From playlist MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015

Transverse Measures and Best Lipschitz and Least Gradient Maps - Karen Uhlenbeck
Analysis Seminar Topic: Transverse Measures and Best Lipschitz and Least Gradient Maps Speaker: Karen Uhlenbeck Affiliation: University of Texas, Austin; Distinguished Visiting Professor, School of Mathematics Date: November 09, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Distance point and plane the Lagrange way
In this video, I derive the formula for the distance between a point and a plane, but this time using Lagrange multipliers. This not only gives us a neater way of solving the problem, but also gives another illustration of the method of Lagrange multipliers. Enjoy! Note: Check out this vi
From playlist Partial Derivatives

Which path should you take? | Introduction to Calculus of Variations
Which path should you take? An introduction to Calculus of Variations. animations / visuals made using: manim: https://github.com/ManimCommunity/manim/ gslides: http://slides.google.com/ written math: my unprofessional tablet setup :3 social media stuff: webstie: https://ongzz.me instagr
From playlist Summer of Math Exposition Youtube Videos

Planck Scale as a Constant of Integration by Alexander Vikman
PROGRAM: PHYSICS OF THE EARLY UNIVERSE - AN ONLINE PRECURSOR ORGANIZERS: Robert Brandenberger (McGill University, Montreal, Canada), Jerome Martin (Institut d'Astrophysique de Paris, France), Subodh Patil (Instituut-Lorentz for Theoretical Physics, Leiden, Netherlands) and L Sriramkumar (
From playlist Physics of The Early Universe - An Online Precursor

Ari Stern: Hybrid finite element methods preserving local symmetries and conservation laws
Abstract: Many PDEs arising in physical systems have symmetries and conservation laws that are local in space. However, classical finite element methods are described in terms of spaces of global functions, so it is difficult even to make sense of such local properties. In this talk, I wil
From playlist Numerical Analysis and Scientific Computing

Liam Mazurowski - Recent developments in constant mean curvature hypersurfaces II
Continuing from the previous talk, we will first discuss two min-max theorems for constructing prescribed mean curvature hypersurfaces in non-compact spaces. The first concerns the existence of prescribed mean curvature hypersurfaces in Euclidean space, and the second concerns the existen
From playlist Not Only Scalar Curvature Seminar

Jean-Frédéric Gerbeau: Fluid-structure interaction in the cardiovascular system. Lecture 2
Abstract: I will introduce the topic of computational cardiac electrophysiology and electrocardiograms simulation. Then I will address some questions of general interest, like the modeling of variability and the extraction of features from biomedical signals, relevant for identification an
From playlist Mathematics in Science & Technology

Chapter 3: Lagrange's theorem, Subgroups and Cosets | Essence of Group Theory
Lagrange's theorem is another very important theorem in group theory, and is very intuitive once you see it the right way, like what is presented here. This video also discusses the idea of subgroups and cosets, which are crucial in the development of the Lagrange's theorem. Other than c
From playlist Essence of Group Theory

