
Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)
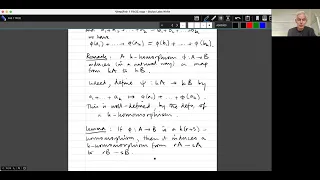
Introduction to additive combinatorics lecture 5.8 --- Freiman homomorphisms and isomorphisms.
The notion of a Freiman homomorphism and the closely related notion of a Freiman isomorphism are fundamental concepts in additive combinatorics. Here I explain what they are and prove a lemma that states that a subset A of F_p^N such that kA - kA is not too large is "k-isomorphic" to a sub
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Commutative algebra 59: Krull's principal ideal theorem
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We give some applications of the theorems we proved about the dimension of local rings. We first show that the dimension of a
From playlist Commutative algebra

Commutative algebra 58: System of parameters versus Krull
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We show that the smallest size of a system of parameters of a Noetherian local ring is at most the Krull dimension. The proof
From playlist Commutative algebra

Commutative algebra 57: Krull versus Hilbert
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We continue the previous video by showing that the Krull dimension of a Noetherian local ring is at most the dimension defined
From playlist Commutative algebra

Commutative algebra 55: Dimension of local rings
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We give 4 definitions of the dimension of a Noetherian local ring: Brouwer-Menger-Urysohn dimension, Krull dimension, degree o
From playlist Commutative algebra

Origin and Development of Valuation Theory by Sudesh Khanduja
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Emmy Noether in Erlangen and Göttingen by Ravi Rao
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

From cluster categories to scattering diagrams (Lecture 1) by Bernhard Keller
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics

P. Scholze - p-adic K-theory of p-adic rings
The original proof of Grothendieck's purity conjecture in étale cohomology (the Thomason-Gabber theorem) relies on results on l-adic K-theory and its relation to étale cohomology when l is invertible. Using recent advances of Clausen-Mathew-Morrow and joint work with Bhatt and Morrow, our
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday

The Campbell-Baker-Hausdorff and Dynkin formula and its finite nature
In this video explain, implement and numerically validate all the nice formulas popping up from math behind the theorem of Campbell, Baker, Hausdorff and Dynkin, usually a.k.a. Baker-Campbell-Hausdorff formula. Here's the TeX and python code: https://gist.github.com/Nikolaj-K/8e9a345e4c932
From playlist Algebra

The Curse of Oak Island: TWO HUGE FINDS IN ONE DAY (Season 8) | History
While continuing to excavate more sections of the stone pathway, the team stumbles upon two significant finds - a cuff button and an old fire grate, in this clip from Season 8, "Off the Railing." #OakIsland Watch all new episodes of The Curse of Oak Island, Tuesdays at 9/8c, and stay up
From playlist Forged in Fire: Season 8 | New Episodes Return Wednesday, March 24 at 9/8c | History

The Curse of Oak Island: MYSTERIOUS METAL Reveals Secret Hatch Location (Season 9)
Gary Drayton and the team uncover compelling clues in their search for the hatch location, in this clip from Season 9, "The Root Cause." Watch the new episodes of The Curse of Oak Island, Tuesdays at 9/8c, and stay up to date on all of your favorite The HISTORY Channel shows at history.co
From playlist The Curse of Oak Island: Season 9 | History
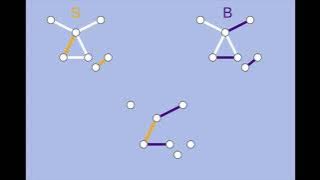
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

The Curse of Oak Island: HIDDEN INSCRIPTION Linked to Knights Templar (Season 9)
The team travels to Portugal to investigate some potentially important clues that tie back to the Knights Templar, in this clip from Season 9, "Follow the Cobblestone Road." Watch the new episodes of The Curse of Oak Island, Tuesdays at 9/8c, and stay up to date on all of your favorite Th
From playlist The Curse of Oak Island: Season 9 | History

Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants