
Introduction to Euler's Totient Function!
Euler's totient function φ(n) is an important function in number theory. Here we go over the basics of the definition of the totient function as well as the value for prime numbers and powers of prime numbers! Modular Arithmetic playlist: https://www.youtube.com/playlist?list=PLug5ZIRrShJ
From playlist Modular Arithmetic

(New Version Available) Inverse Functions
New Version: https://youtu.be/q6y0ToEhT1E Define an inverse function. Determine if a function as an inverse function. Determine inverse functions. http://mathispower4u.wordpress.com/
From playlist Exponential and Logarithmic Expressions and Equations

Ex 1: Find the Inverse of a Function
This video provides two examples of how to determine the inverse function of a one-to-one function. A graph is used to verify the inverse function was found correctly. Library: http://mathispower4u.com Search: http://mathispower4u.wordpress.com
From playlist Determining Inverse Functions

Define an inverse function. Determine if a function as an inverse function. Determine inverse functions.
From playlist Determining Inverse Functions

Totient Function - Applied Cryptography
This video is part of an online course, Applied Cryptography. Check out the course here: https://www.udacity.com/course/cs387.
From playlist Applied Cryptography

Ex 2: Find the Inverse of a Function
This video provides two examples of how to determine the inverse function of a one-to-one function. A graph is used to verify the inverse function was found correctly. Library: http://mathispower4u.com Search: http://mathispower4u.wordpress.com
From playlist Determining Inverse Functions

a pyramid fact about functions
In this video, I give a nice application of the Intermediate Value Theorem: Namely if f is continuous on [0,2] and f(0) = f(2), we can actually find x and y with |x-y| = 1 such that f(x) = f(y). So functions as such have a "pyramid" structure. Enjoy! IVT: https://youtu.be/0XWIFPbI05k IVT
From playlist Limits and Continuity

ʕ•ᴥ•ʔ Implicit Differentiation: Easy Foundation and Simple Examples
Quickly master Implicit Differentiation with easy foundation and simple examples. Watch more lessons like this and try our practice at https://www.studypug.com/calculus-help/derivatives/implicit-differentiation An inverse function is a function that reverses all the operations of another
From playlist UK Year 12 Maths

Discrete Structures: Multiplicative Inverse; Greatest Common Divisor; Euler's Totient Function
Decrypting the linear cipher leaves us with a fundamental problem: dividing two integers yields a fraction, which is difficult to work with. Learn about new concepts: the greatest common divisor (GCD), the multiplicative inverse, and Euler's totient function. These will allow us to decrypt
From playlist Discrete Structures, Spring 2022

Explicit Formula for Euler's Totient Function!
Totient of p^a: https://youtu.be/NgZ33qr5WHM?t=210 Product formula: https://youtu.be/qpYqvNBQZ4g Euler's totient function involves counting how many numbers are coprime to n. In fact, we can calculate this value directly as long as we know the prime factors! This makes many theorems in n
From playlist Modular Arithmetic

AKPotW: A Lack of Primitive Roots [Number Theory]
If this video is confusing, be sure to check out our blog for the full solution transcript! https://centerofmathematics.blogspot.com/2018/05/advanced-knowledge-problem-of-week-5-3.html
From playlist Center of Math: Problems of the Week

Math 030 Calculus I 031315: Inverse Functions and Differentiation
Inverse functions. Examples of determining the inverse. Relation between the graphs of a function and its inverse. One-to-one functions. Restricting the domain of a function so that it is invertible. Differentiability of inverse functions; relation between derivatives of function and
From playlist Course 2: Calculus I

Asymmetric Key Cryptography: The RSA Algorithm by Hand
This video demonstrates the underlying principles of the RSA cryptosystem. It shows how the public and private asymmetric keys can be calculated from a pair of prime numbers. It also shows how to encrypt a message using the public key, and decrypt it using the private key. For ease, the
From playlist Cryptography

Proof that the Totient Function is Multiplicative
Coprime numbers mod n: https://youtu.be/SslPWR2N5jA Chinese remainder theorem: https://www.youtube.com/playlist?list=PL22w63XsKjqyg3TEfDGsWoMQgWMUMjYhl Surjection and bijection: https://youtu.be/kt5eABzTVGQ Explanation of why Euler's totient function of a product of coprime numbers is e
From playlist Modular Arithmetic

Discrete Structures: Public Key Cryptography; RSA
See that little "lock" icon in your browser's address bar? What does that mean? Learn about the RSA algorithm, how it helps solve the key-exchange problem, and how your browser uses these algorithms to protect your privacy.
From playlist Discrete Structures, Spring 2022

GT12. Aut(Z/n) and Fermat's Little Theorem
Abstract Algebra: We show that Aut(Z/n) is isomorphic to (Z/n)*, the group of units in Z/n. In turn, we show that the units consist of all m in Z/n with gcd(m,n)=1. Using (Z/n)*, we define the Euler totient function and state and prove Fermat's Little Theorem: if p is a prime, then, for
From playlist Abstract Algebra

Discrete Structures: Digital certificates and implementing RSA
Our last session on RSA and public key cryptography. We'll learn about digital certificates and see how to implement the core RSA algorithms in Python.
From playlist Discrete Structures, Spring 2022
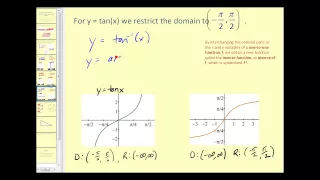
Introduction to Inverse Sine, Inverse Cosine, and Inverse Tangent
Introduction to the inverse functions of sine, cosine, and tangent http://mathispower4u.wordpress.com/
From playlist Inverse Trigonometric Functions

Eulers Theorem - Applied Cryptography
This video is part of an online course, Applied Cryptography. Check out the course here: https://www.udacity.com/course/cs387.
From playlist Applied Cryptography