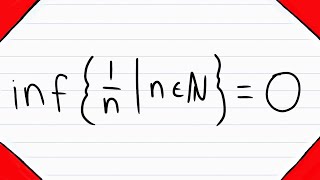
Infimum and supremum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset of a partially ordered set is a greatest element in that is less than or equal to each element of if such an element exists. Consequently, the term greatest lower bound (abbreviated as GLB) is also commonly used. The supremum (abbreviated sup; plural suprema) of a subset of a partially ordered set is the least element in that is greater than or equal to each element of if such an element exists. Consequently, the supremum is also referred to as the least upper bound (or LUB). The infimum is in a precise sense dual to the concept of a supremum. Infima and suprema of real numbers are common special cases that are important in analysis, and especially in Lebesgue integration. However, the general definitions remain valid in the more abstract setting of order theory where arbitrary partially ordered sets are considered. The concepts of infimum and supremum are close to minimum and maximum, but are more useful in analysis because they better characterize special sets which may have no minimum or maximum. For instance, the set of positive real numbers (not including ) does not have a minimum, because any given element of could simply be divided in half resulting in a smaller number that is still in There is, however, exactly one infimum of the positive real numbers relative to the real numbers: which is smaller than all the positive real numbers and greater than any other real number which could be used as a lower bound. An infimum of a set is always and only defined relative to a superset of the set in question. For example, there is no infimum of the positive real numbers inside the positive real numbers (as their own superset), nor any infimum of the positive real numbers inside the complex numbers with positive real part. (Wikipedia).