
A02 Independence of the solution set
The independence of a linear system. How to make sure that a set of solutions are not constant multiples of each other.
From playlist A Second Course in Differential Equations

Further examination of independence
From playlist Unit 5 Probability A: Basic Probability

More Help with Independence Part 2Indep FE pt 2
More insight into the probability concept of independence
From playlist Unit 5 Probability A: Basic Probability
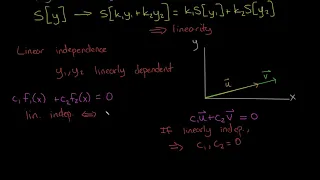
Differential Equations: Linear Independence
Linear independence is a core idea from Linear Algebra. Surprisingly, it's also important in differential equations. This video is the second precursor to our discussion of homogeneous differential equations.
From playlist Differential Equations
Region between x^2+y^2 and 2x+y+1
From playlist Triple integrals
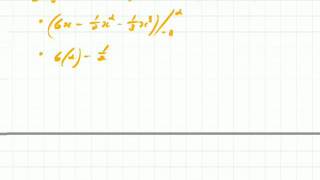
Integration 4 The Definite Integral Part 3 Example 1
An example using the definite integral.
From playlist Integration

(0:00) Independence of two events (4:12) (Mutual) Independence of multiple events (9:30) Conditional Independence of two events A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4
From playlist Probability Theory

Integration 4 The Definite Integral Part 2
Working through an example of the definite integral
From playlist Integration

Calculus 3: Line Integrals (34 of 44) Condition 1 for Independence
Visit http://ilectureonline.com for more math and science lectures! In this video I will define Condition 1 necessary of path Independence for paths 1,2 of 2 for vector field F=(y)i+(x)j. Next video in the series can be seen at: https://youtu.be/H5g4byUd6qc
From playlist CALCULUS 3 CH 6 LINE INTEGRALS

Jonathan Barmak: Star clusters in clique complexes and the Vietoris-Rips complex of planar sets
Abstract: The star cluster of a simplex in a simplicial complex K is the union of the stars of its vertices. When K is clique, star clusters are contractible. We will recall applications of this notion to the study of homotopy invariants of independence complexes of graphs. If X is a plan
From playlist Vietoris-Rips Seminar
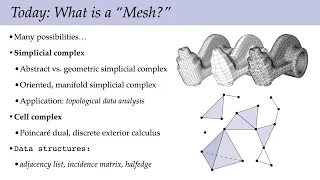
Lecture 2A: What is a "Mesh?" (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Spectral Independence in High-dimensional Expanders and Applications... - Kuikui Liu
Computer Science/Discrete Mathematics Seminar II Topic: Spectral Independence in High-dimensional Expanders and Applications to the Hardcore Model Speaker: Kuikui Liu Affiliation: University of Washington Date: February 27, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics
Strongly log concave polynomials...Bases of Matroids - Shayan Oveis Gharan
More videos on http://video.ias.edu
From playlist Mathematics

Complex sentences | Syntax | Khan Academy
Keep going! Check out the next lesson and practice what you’re learning: https://www.khanacademy.org/humanities/grammar/syntax-sentences-and-clauses/types-of-sentences/v/compound-complex-sentences-syntax-khan-academy Complex sentences are simple sentences with dependent or subordinate cla
From playlist Grammar

Johnathan Bush (11/5/21): Maps of Čech and Vietoris–Rips complexes into euclidean spaces
We say a continuous injective map from a topological space to k-dimensional euclidean space is simplex-preserving if the image of each set of at most k+1 distinct points is affinely independent. We will describe how simplex-preserving maps can be useful in the study of Čech and Vietoris–Ri
From playlist Vietoris-Rips Seminar

Daniel Kral: Parametrized approach to block structured integer programs
Integer programming is one of the most fundamental problems in discrete optimization. While integer programming is computationally hard in general, there exist efficient algorithms for special instances. In particular, integer programming is fixed parameter tractable when parameterized by
From playlist Workshop: Parametrized complexity and discrete optimization

A problem in Elementary Geometry - Michael Atiyah [2011]
Name: Michael Atiyah Event: SCGP Weekly Talk Title: A problem in Elementary Euclidean Geometry Date: 2011-10-25 @1:00 PM Location: 103 Abstract: Over a decade ago I stumbled across a new and apparently very elementary problem in Euclidean Geometry involving n distinct points in 3-space. E
From playlist Mathematics

What is an integral and it's parts
👉 Learn about integration. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which the upper and the lower li
From playlist The Integral

Shu Kanazawa (7/6/2020): A limit theorem for Betti numbers of random simplicial complexes
Title: A limit theorem for Betti numbers of homogeneous and spatially independent random simplicial complexes Abstract: The Erdős–Rényi graph model has been extensively studied since the 1960s as a typical random graph model. Recently, the study of random simplicial complexes has drawn at
From playlist ATMCS/AATRN 2020