Immersed boundary method

Computational fluid dynamics | Numerical differential equations

In computational fluid dynamics, the immersed boundary method originally referred to an approach developed by Charles Peskin in 1972 to simulate fluid-structure (fiber) interactions. Treating the coupling of the structure deformations and the fluid flow poses a number of challenging problems for numerical simulations (the elastic boundary changes the flow of the fluid and the fluid moves the elastic boundary simultaneously). In the immersed boundary method the fluid is represented in an Eulerian coordinate system and the structure is represented in Lagrangian coordinates. For Newtonian fluids governed by the Navier–Stokes equations, the fluid equations are and if the flow is incompressible, we have the further condition that The immersed structures are typically represented as a collection of one-dimensional fibers, denoted by . Each fiber can be viewed as a parametric curve where is the Lagrangian coordinate along the fiber and is time. The physics of the fiber is represented via a fiber force distribution function . Spring forces, bending resistance or any other type of behavior can be built into this term. The force exerted by the structure on the fluid is then interpolated as a source term in the momentum equation using where is the Dirac δ function. The forcing can be extended to multiple dimensions to model elastic surfaces or three-dimensional solids. Assuming a massless structure, the elastic fiber moves with the local fluid velocity and can be interpolated via the delta function where denotes the entire fluid domain. Discretization of these equations can be done by assuming an Eulerian grid on the fluid and a separate Lagrangian grid on the fiber. Approximations of the Delta distribution by smoother functions will allow us to interpolate between the two grids. Any existing fluid solver can be coupled to a solver for the fiber equations to solve the Immersed Boundary equations.Variants of this basic approach have been applied to simulate a wide variety of mechanical systems involving elastic structures which interact with fluid flows. Since the original development of this method by Peskin, a variety of approaches have been developed to simulate flow over complicated immersed bodies on grids that do not conform to the surface of the body. These include methods such as the immersed interface method, the Cartesian grid method, the ghost fluid method and the cut-cell method. Mittal and Iaccarino refer to all these (and other related) methods as Immersed Boundary Methods and provide various categorizations of these methods. From the point of view of implementation, they categorize immersed boundary methods into continuous forcing and discrete forcing methods. In the former, a force term is added to the continuous Navier-Stokes equations before discretization, whereas in the latter, the forcing is applied (explicitly or implicitly) to the discretized equations. Under this taxonomy, Peskin's original method is a continuous forcing method whereas Cartesian grid, cut-cell and the ghost-fluid methods are discrete forcing methods. (Wikipedia).

Linear Desface

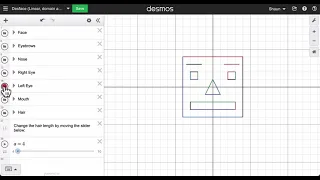
Here we show a quick way to set up a face in desmos using domain and range restrictions along with sliders. @shaunteaches

From playlist desmos

How plunger pump works (Must Watch). ✔

More details visit: http://www.techtrixinfo.com/ Working of a Plunger Pump, it is a type of Reciprocating pump. This is a reciprocating type of pump. Was used in automobiles as lubrication pumps in the earlier days, now it's obsolesce. Main components if a Plunger pump are: Plunger.

From playlist Hydraulics and related stuff.

Mechanical Engineering: Forces on Submerged Surfaces (2 of 15) Vertical Wall Integration

Visit http://ilectureonline.com for more math and science lectures! In this video I will use integration to find the pressure and average pressure of water on a vertical wall. Next video in this series can be seen at: https://youtu.be/o_0ZH9l5d_M

From playlist MECHANICAL ENGINEERING 6 FORCES ON SUBMERGED SURFACES

How to find all of the solutions to an equation as well as within the unit circle

👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric identities, they include by factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the give

From playlist Solve Trigonometric Equations

How to find all of the solutions of an equation with secant

From playlist Solve Trigonometric Equations

Find all the solutions of trig equation with cotangent

👉 Learn how to solve trigonometric equations. There are various methods that can be used to evaluate trigonometric equations, they include by factoring out the GCF and simplifying the factored equation. Another method is to use a trigonometric identity to reduce and then simplify the given

From playlist Solve Trigonometric Equations

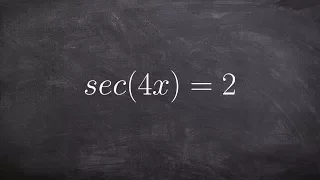
Solving trigonometric equations with multiple angles

From playlist Solve Trigonometric Equations with Multi Angles

Solving trigonometric equations with multiple angles

From playlist Solve Trigonometric Equations with Multi Angles

Stable hypersurfaces with prescribed mean curvature -Costante Bellettini

Variational Methods in Geometry Seminar Topic: Stable hypersurfaces with prescribed mean curvature Speaker: Costante Bellettini Affiliation: Princeton University; Member, School of Mathematics Date: April 2, 2019 For more video please visit http://video.ias.edu

From playlist Variational Methods in Geometry

FEM@LLNL | Topics in Immersed Boundary and Contact Interface Methods

Sponsored by the MFEM project, the FEM@LLNL Seminar Series focuses on finite element research and applications talks of interest to the MFEM community. On May 24, 2022, Mike Puso of LLNL presented "Topics in Immersed Boundary and Contact Interface Methods: Current LLNL Projects and Resear

From playlist FEM@LLNL Seminar Series

FEM@LLNL | The Shifted Boundary Method: An Immersed Approach for Computational Mechanics

Sponsored by the MFEM project, the FEM@LLNL Seminar Series focuses on finite element research and applications talks of interest to the MFEM community. On January 20, 2022, Dr. Guglielmo Scovazzi of Duke University presented "The Shifted Boundary Method: An Immersed Approach for Computati

From playlist FEM@LLNL Seminar Series

Regularity of the limit set of embedded Poincaré Disks - Vincent Borelli

Workshop on the h-principle and beyond Topic: Regularity of the limit set of embedded Poincaré Disks Speaker: Vincent Borelli Affiliation: University of Lyon Date: November 4, 2021 Abstract: Let f be an embedding of a non compact manifold into an Euclidean space and p_n be a divergent se

From playlist Mathematics

D. Stern - Harmonic map methods in spectral geometry (version temporaire)

Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to connections to the study of sphere-valued harmonic maps and minimal immersions. In this talk, I'll

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

8ECM Plenary Lecture: Franc Forstnerič

From playlist 8ECM Plenary Lectures

D. Stern - Harmonic map methods in spectral geometry

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Minimal surfaces in R^3 and Maximal surfaces in L^3 (Lecture 2) by Pradip Kumar

ORGANIZERS : C. S. Aravinda and Rukmini Dey DATE & TIME : 16 June 2018 to 25 June 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore This workshop on geometry and topology for lecturers is aimed for participants who are lecturers in universities/institutes and colleges in India. This w

From playlist Geometry and Topology for Lecturers

Hydraulic cylinder with fixed piston

Green cylinder with machine table reciprocates. Pressure fluid is conducted into cylinder via holes on fixed piston rod. The hoses can be stationary. In case using holes on the cylinder the hoses have to move with the cylinder. The arrows show flows of pressure fluid.

From playlist Mechanisms

Daniel T. Wise - 2/6 CAT(o) Cube Complexes

From playlist Summer School 2019: Aspects of Geometric Group Theory

Learn how to find all the solutions to a trigonometric equation

From playlist Solve Trigonometric Equations

Recent advances in Geometric Analysis - 8 June 2018

http://crm.sns.it/event/435 Centro di Ricerca Matematica Ennio De Giorgi The aim of the workshop is to bring together experts working on different sides of Geometric Analysis: PDE aspects, minimal or constant mean curvature surfaces, geometric inequalities, applications to general relativ

From playlist Centro di Ricerca Matematica Ennio De Giorgi

Immersed boundary method

Related pages