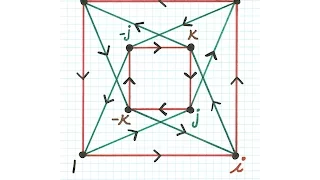
Euler's Formula for the Quaternions
In this video, we will derive Euler's formula using a quaternion power, instead of a complex power, which will allow us to calculate quaternion exponentials such as e^(i+j+k). If you like quaternions, this is a pretty neat formula and a simple generalization of Euler's formula for complex
From playlist Math
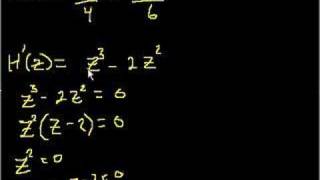
Using the monotonicity theorem to determine when a function is increasing or decreasing.
From playlist Calculus

Marston Morse - An Isoperimetric Concept for the Mass in General Relativity - Gerhard Huisken
Gerhard Huisken Max-Planck Institute for Gravitational Physics March 20, 2009 For more videos, visit http://video.ias.edu
From playlist Mathematics

Yoshihiro Tonegawa: Introduction to Brakke's mean curvature flow (part I)
The lecture was held within the framework of the Hausdorff Trimester Program: Evolution of Interfaces. Abstract: Among numerous evolution problems involving interface, the mean curvature flow stands out for its simplicity, depth, and width of relevant subfields. The aim of this mini-cours
From playlist Winter School on "Interfaces in Geometry and Fluids"

Yoshihiro Tonegawa: Introduction to Brakke's mean curvature flow (part II)
The lecture was held within the framework of the Hausdorff Trimester Program: Evolution of Interfaces. Abstract: Among numerous evolution problems involving interface, the mean curvature flow stands out for its simplicity, depth, and width of relevant subfields. The aim of this mini-cours
From playlist Winter School on "Interfaces in Geometry and Fluids"

Yoshihiro Tonegawa: Introduction to Brakke's mean curvature flow (part III)
The lecture was held within the framework of the Hausdorff Trimester Program: Evolution of Interfaces. Abstract: Among numerous evolution problems involving interface, the mean curvature flow stands out for its simplicity, depth, and width of relevant subfields. The aim of this mini-cours
From playlist Winter School on "Interfaces in Geometry and Fluids"

Yoshihiro Tonegawa: Introduction to Brakke's mean curvature flow (part IV)
The lecture was held within the framework of the Hausdorff Trimester Program: Evolution of Interfaces. Abstract: Among numerous evolution problems involving interface, the mean curvature flow stands out for its simplicity, depth, and width of relevant subfields. The aim of this mini-cours
From playlist Winter School on "Interfaces in Geometry and Fluids"

F. Schulze - Mean curvature flow with generic initial data
Mean curvature flow is the gradient flow of the area functional and constitutes a natural geometric heat equation on the space of hypersurfaces in an ambient Riemannian manifold. It is believed, similar to Ricci Flow in the intrinsic setting, to have the potential to serve as a tool to app
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

F. Schulze - Mean curvature flow with generic initial data (version temporaire)
Mean curvature flow is the gradient flow of the area functional and constitutes a natural geometric heat equation on the space of hypersurfaces in an ambient Riemannian manifold. It is believed, similar to Ricci Flow in the intrinsic setting, to have the potential to serve as a tool to app
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Dimitri Zvonkine - On two ELSV formulas
The ELSV formula (discovered by Ekedahl, Lando, Shapiro and Vainshtein) is an equality between two numbers. The first one is a Hurwitz number that can be defined as the number of factorizations of a given permutation into transpositions. The second is the integral of a characteristic class
From playlist 4th Itzykson Colloquium - Moduli Spaces and Quantum Curves

Pengyu Le - Null hypersurfaces and the Penrose inequality for a perturbed Schwarzschild black hole
Recorded 25 October 2021. Pengyu Le of the University of Michigan presents "Null hypersurfaces and the Penrose inequality for a perturbed Schwarzschild black hole" at IPAM's Workshop II: Mathematical and Numerical Aspects of Gravitation. Abstract: The Penrose inequality is a renowned inequ
From playlist Workshop: Mathematical and Numerical Aspects of Gravitation

How to Determine if Functions are Linearly Independent or Dependent using the Definition
How to Determine if Functions are Linearly Independent or Dependent using the Definition If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Th
From playlist Zill DE 4.1 Preliminary Theory - Linear Equations

When Does Exponentiation Commute ? (Part 2)
In this video, we continue the discussion of finding (x,y) pairs that will commute under exponentiation: x^y = y^x. This time, we will find another way of writing Euler's number and solve the equation x^y = y^x for y with the help of the Lambert W function. Ideas were adapted from the fol
From playlist Math

Determine Solutions to a Linear Equation in Two Variables
This video explains how to determine ordered pair solutions to a linear equation in two variables. http://mathispower4u.com
From playlist The Coordinate Plane, Plotting Points, and Solutions to Linear Equations in Two Variables

The sum over all naturals: Why -1/12 is your friend
In this video I speak about the infamous fraction -1/12 and discuss why and where it pops up. We discuss the Euler-Maclaurin formula, shift-operators and the operator exponential, we touch on Lie algebras, the the Riemann zeta function and - most importantly - the Bernoulli numbers. Here
From playlist Analysis

Math 031 031017 Monotone Sequence Theorem
The rational numbers have holes: square root of 2 is irrational. Bounded sequences; bounded above, bounded below. Q. Does bounded imply convergent? (No.) Q. Does convergent imply bounded? (Yes.) Proof that convergent implies bounded. Statement of Monotone Sequence Theorem. Definition
From playlist Course 3: Calculus II (Spring 2017)
Marston Morse - Inverse Mean Curvature Flow and Isoperimetric Inequalities
Gerhard Huisken Max-Planck Institute for Gravitational Physics March 20, 2009 For more videos, visit http://video.ias.edu
From playlist Mathematics

Calculus 2: Complex Numbers & Functions (23 of 28) What are complex Exponentials? 2
Visit http://ilectureonline.com for more math and science lectures! In this video I will derive the formula for finding complex exponentials, e^(iy)=?, and its relationship to Euler's equation, z=x-iy. Next video in the series can be seen at: https://youtu.be/ZXKG7o7Bpz4
From playlist CALCULUS 2 CH 11 COMPLEX NUMBERS

Lower bounds for subgraph isomorphism – Benjamin Rossman – ICM2018
Mathematical Aspects of Computer Science Invited Lecture 14.3 Lower bounds for subgraph isomorphism Benjamin Rossman Abstract: We consider the problem of determining whether an Erdős–Rényi random graph contains a subgraph isomorphic to a fixed pattern, such as a clique or cycle of consta
From playlist Mathematical Aspects of Computer Science

Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory