
Lie Groups and Lie Algebras: Lesson 39 - The Universal Covering Group
Lie Groups and Lie Algebras: Lesson 39 - The Universal Covering Group We are finally in position to understand the nature of the Universal Covering Group and its connection to all the Lie groups which share a single Lie algebra. This is a critical lecture! In this lecture we simply state
From playlist Lie Groups and Lie Algebras

This lecture is part of an online graduate course on Lie groups. We give an introductory survey of Lie groups theory by describing some examples of Lie groups in low dimensions. Some recommended books: Lie algebras and Lie groups by Serre (anything by Serre is well worth reading) Repre
From playlist Lie groups

Why Are Prejudice and Conflict So Common? | Understanding the Mysteries of Human Behavior
It's no wonder discrimination seems to be everywhere: splitting people into two groups, even at random, makes them subconsciously dislike each other. A sense of competition can exaggerate these feelings. Pick up your tools; we've got some bridge building to do. Presented by Mark Leary Lea
From playlist Latest Uploads
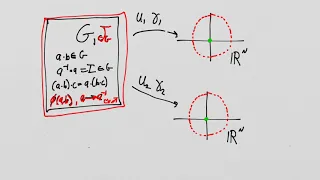
Lie Groups and Lie Algebras: Lesson 38 - Preparation for the concept of a Universal Covering Group
Lie Groups and Lie Algebras: Lesson 38 - Preparation for the Universal Covering Group concept In this lesson we examine another amazing connection between the algebraic properties of the Lie groups with topological properties. We will lay the foundation to understand how discrete invaria
From playlist Lie Groups and Lie Algebras
Grothendieck Pairs and Profinite Rigidity - Martin Bridson
Arithmetic Groups Topic: Grothendieck Pairs and Profinite Rigidity Speaker: Martin Bridson Affiliation: Oxford University Date: January 26, 2022 If a monomorphism of abstract groups H↪G induces an isomorphism of profinite completions, then (G,H) is called a Grothendieck pair, recalling t
From playlist Mathematics

Regular permutation groups and Cayley graphs
Cheryl Praeger (University of Western Australia). Plenary Lecture from the 1st PRIMA Congress, 2009. Plenary Lecture 11. Abstract: Regular permutation groups are the 'smallest' transitive groups of permutations, and have been studied for more than a century. They occur, in particular, as
From playlist PRIMA2009

On the pioneering works of Professor I.B.S. Passi by Sugandha Maheshwari
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Vincent Guirardel: Natural subgroups of automorphisms
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebra

Gilbert Levitt - Vertex finiteness for relatively hyperbolic groups
Gilbert Levitt (University of Caen, France) Given a finitely generated group G, we consider all splittings of G over subgroups in a fixed family (such as finite groups, cyclic groups, abelian groups). We discuss whether it is the case that only finitely many vertex groups appear, up to is
From playlist T1-2014 : Random walks and asymptopic geometry of groups.

Group actions on 1-manifolds: A list of very concrete open questions – Andrés Navas – ICM2018
Dynamical Systems and Ordinary Differential Equations Invited Lecture 9.8 Group actions on 1-manifolds: A list of very concrete open questions Andrés Navas Abstract: Over the last four decades, group actions on manifolds have deserved much attention by people coming from different fields
From playlist Dynamical Systems and ODE









