
Maximum modulus principle In this video, I talk about the maximum modulus principle, which says that the maximum of the modulus of a complex function is attained on the boundary. I also show that the same thing is true for the real and imaginary parts, and finally I discuss the strong max
From playlist Complex Analysis

Maximum principle for heat equation In this video, I present the maximum principle, which is a very interesting property of the heat equation: Namely the largest (and smallest) value of solutions is attained either initially, or on the sides! Check out my PDE Playlist: https://www.yout
From playlist Partial Differential Equations

Free ebook https://bookboon.com/en/partial-differential-equations-ebook What is the maximum principle for partial differential equations and how is it useful? The main result is presented and proved. Such ideas have important applications to understanding the behaviour of solutions to pa
From playlist Partial differential equations

Extreme Value Theorem Using Critical Points
Calculus: The Extreme Value Theorem for a continuous function f(x) on a closed interval [a, b] is given. Relative maximum and minimum values are defined, and a procedure is given for finding maximums and minimums. Examples given are f(x) = x^2 - 4x on the interval [-1, 3], and f(x) =
From playlist Calculus Pt 1: Limits and Derivatives
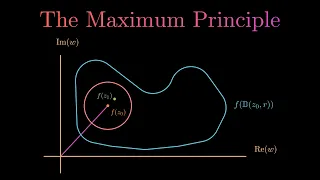
MAXIMUM PRINCIPLE -- Part 1 -- Core Theorems of Complex Analysis
Part 2: https://www.youtube.com/watch?v=jmP4VlgZvb0 Part 3: https://www.youtube.com/watch?v=fLnRDhhzWKQ In this video, we give a proof of the Maximum Principle, which is a monumental result in the subject of complex analysis. The maximum principle is also referred to as the maximum modul
From playlist Complex Analysis

Maximum and Maximal Cliques | Graph Theory, Clique Number
What are maximum cliques and maximal cliques in graph theory? We'll be defining both terms in today's video graph theory lesson, as well as going over an example of finding maximal and maximum cliques in a graph. These two terms can be a little confusing, so let's dig in and clarify our un
From playlist Graph Theory
Maximum and Minimum of a set In this video, I define the maximum and minimum of a set, and show that they don't always exist. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh
From playlist Real Numbers

Maximum and Minimum Values (Closed interval method)
A review of techniques for finding local and absolute extremes, including an application of the closed interval method
From playlist 241Fall13Ex3

Absolute Maximum/Minimum (1 of 2: Domain restricted polynomial)
More resources available at www.misterwootube.com
From playlist Applications of Differentiation

Harmonic Maps between surfaces and Teichmuller theory (Lecture - 2) by Michael Wolf
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Yat Tin Chow: "A numerical method of solving high dimensional Hamilton-Jacobi equations with gen..."
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop I: High Dimensional Hamilton-Jacobi Methods in Control and Differential Games "A numerical method of solving high dimensional Hamilton-Jacobi equations with generalized Hopf-Lax formula" Yat Tin Chow - University of California, Riverside
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Neural oscillations, weak coupling and networks by Bard Ermentrout
Dynamics of Complex Systems - 2017 DATES: 10 May 2017 to 08 July 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore This Summer Program on Dynamics of Complex Systems is second in the series. The theme for the program this year is Mathematical Biology. Over the past decades, the focus o
From playlist Dynamics of Complex Systems - 2017

Steve Brunton: "Discovering interpretable and generalizable dynamical systems from data"
Machine Learning for Physics and the Physics of Learning 2019 Workshop III: Validation and Guarantees in Learning Physical Models: from Patterns to Governing Equations to Laws of Nature "Discovering interpretable and generalizable dynamical systems from data" Steve Brunton - University of
From playlist Machine Learning for Physics and the Physics of Learning 2019

Lionel Roques: Uniqueness of coefficients by strong maximum principle
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Partial Differential Equations

Harmonic Maps between surfaces and Teichmuller theory (Lecture - 1) by Michael Wolf
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Population dynamics by Jeff Gore
Winter School on Quantitative Systems Biology DATE:04 December 2017 to 22 December 2017 VENUE:Ramanujan Lecture Hall, ICTS, Bengaluru The International Centre for Theoretical Sciences (ICTS) and the Abdus Salam International Centre for Theoretical Physics (ICTP), are organizing a Winter S
From playlist Winter School on Quantitative Systems Biology

Cylindrical contact homology in dimension 3 via intersection theory and more - Joanna Nelson
Joanna Nelson Member, School of Mathematics October 1, 2014 More videos on http://video.ias.edu
From playlist Mathematics
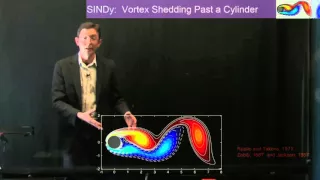
Sparse Identification of Nonlinear Dynamics (SINDy)
This video illustrates a new algorithm for the sparse identification of nonlinear dynamics (SINDy). In this work, we combine machine learning, sparse regression, and dynamical systems to identify nonlinear differential equations purely from measurement data. From the Paper: Discovering
From playlist Research Abstracts from Brunton Lab

Calculus: Absolute Maximum and Minimum Values
In this video, we discuss how to find the absolute maximum and minimum values of a function on a closed interval.
From playlist Calculus

The Hopf Fibration via Higher Inductive Types - Peter Lumsdaine
Peter Lumsdaine Dalhousie University; Member, School of Mathematics February 13, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics