
An interesting homotopy (in fact, an ambient isotopy) of two surfaces.
From playlist Algebraic Topology

Computing homology groups | Algebraic Topology | NJ Wildberger
The definition of the homology groups H_n(X) of a space X, say a simplicial complex, is quite abstract: we consider the complex of abelian groups generated by vertices, edges, 2-dim faces etc, then define boundary maps between them, then take the quotient of kernels mod boundaries at each
From playlist Algebraic Topology

Homotopy type theory: working invariantly in homotopy theory -Guillaume Brunerie
Short talks by postdoctoral members Topic: Homotopy type theory: working invariantly in homotopy theory Speaker: Guillaume Brunerie Affiliation: Member, School of Mathematics Date: September 26, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Algebraic Topology - 11.3 - Homotopy Equivalence
We sketch why that the homotopy category is a category.
From playlist Algebraic Topology
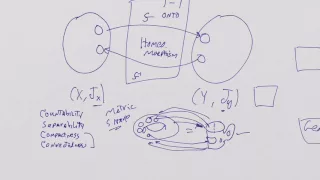
What is a Manifold? Lesson 5: Compactness, Connectedness, and Topological Properties
The last lesson covering the topological prep-work required before we begin the discussion of manifolds. Topics covered: compactness, connectedness, and the relationship between homeomorphisms and topological properties.
From playlist What is a Manifold?

What is a Manifold? Lesson 18: Homotopy
What is a Manifold? Lesson 18: Introduction to Homotopy
From playlist What is a Manifold?
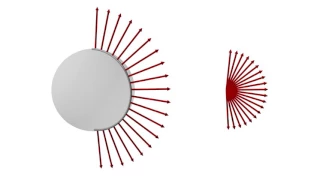
Homotopy elements in the homotopy group π₂(S²) ≅ ℤ. Roman Gassmann and Tabea Méndez suggested some improvements to my original ideas.
From playlist Algebraic Topology

Introduction to Homotopy Theory- PART 1: UNIVERSAL CONSTRUCTIONS
The goal of this series is to develop homotopy theory from a categorical perspective, alongside the theory of model categories. We do this with the hope of eventually developing stable homotopy theory, a personal goal a passion of mine. I'm going to follow nLab's notes, but I hope to add t
From playlist Introduction to Homotopy Theory

Matthew Hedden - Irreducible homology S1xS2's which aren't zero surgeries on a knot
June 20, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry I'll discuss constructions of manifolds with the homology of S^1xS^2 which don't arise as Dehn surgery on a knot in S^3. Our examples have weight one
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry I

Homology cobordism and triangulations – Ciprian Manolescu – ICM2018
Geometry | Topology Invited Lecture 5.5 | 6.1 Homology cobordism and triangulations Ciprian Manolescu Abstract: The study of triangulations on manifolds is closely related to understanding the three-dimensional homology cobordism group. We review here what is known about this group, with
From playlist Geometry

Contact invariants in sutured monopole and instanton homology - Steven Sivek
Steven Sivek University of Warwick March 5, 2014 Kronheimer and Mrowka recently used monopole Floer homology to define an invariant of sutured manifolds, following work of Juhász in Heegaard Floer homology. In this talk, I will construct an invariant of a contact structure on a 3-manifold
From playlist Mathematics

[BOURBAKI 2019] Manolescu’s work on the triangulation conjecture - Stipsicz - 15/06/19
András STIPSICZ Manolescu’s work on the triangulation conjecture The triangulation conjecture (asking whether a manifold is necessarily a simplicial complex) has been recently resolved in the negative by Ciprian Manolescu. His proof is based on work of Galweski–Stern and Matumoto, reduci
From playlist BOURBAKI - 2019

Rustam Sadykov (1/28/21): On the Lusternik-Schnirelmann theory of 4-manifolds
Title: On the Lusternik-Schnirelmann theory of 4-manifolds Abstract: I will discuss various versions of the Lusternik-Schnirelman category involving covers and fillings of 4-manifolds by various sets. In particular, I will discuss Gay-Kirby trisections, which are certain decompositions o
From playlist Topological Complexity Seminar

Symplectic Instanton Homology of Knots and Links in 3-manifolds - David White
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Symplectic Instanton Homology of Knots and Links in 3-manifolds Speaker: David White Affiliation: North Carolina State University Date: February 10, 2023 Powerful homology invariants of knots in 3-manifolds
From playlist Mathematics

Classification of n-component links with Khovanov homology of rank 2^n - Boyu Zhang
Symplectic Dynamics/Geometry Seminar Topic: Classification of n-component links with Khovanov homology of rank 2^n Speaker: Boyu Zhang Affiliation: Princeton University Date: February 24, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Nathan Dunfield, Lecture 3: Floer Homology and Taut Foliations of Hyperbolic 3-Manifolds
33rd Workshop in Geometric Topology, Colorado College, June 11, 2016
From playlist Nathan Dunfield: 33rd Workshop in Geometric Topology
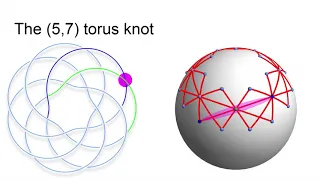
Knots, three-manifolds and instantons – Peter Kronheimer & Tomasz Mrowka – ICM2018
Plenary Lecture 11 Knots, three-manifolds and instantons Peter Kronheimer & Tomasz Mrowka Abstract: Over the past four decades, input from geometry and analysis has been central to progress in the field of low-dimensional topology. This talk will focus on one aspect of these developments
From playlist Plenary Lectures

An introduction to homology | Algebraic Topology | NJ Wildberger
We briefly describe the higher homotopy groups which extend the fundamental group to higher dimensions, trying to capture what it means for a space to have higher dimensional holes. Homology is a commutative theory which also deals with this issue, assigning to a space X a series of homolo
From playlist Algebraic Topology
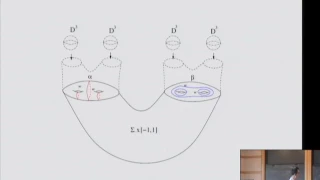
Computations of Heegaard Floer Homologies - Andras Stipsicz
Computations of Heegaard Floer Homologies Andras Stipsicz Renyi Institute of Mathematics, Hungarian Academy of Sciences April 9, 2012 Heegaard Floer homology groups were recently introduced by Ozsvath and Szabo to study properties of 3-manifolds and knots in them. The definition of the inv
From playlist Members Seminar
