
Intro to Linear Systems: 2 Equations, 2 Unknowns - Dr Chris Tisdell Live Stream
Free ebook http://tinyurl.com/EngMathYT Basic introduction to linear systems. We discuss the case with 2 equations and 2 unknowns. A linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that ar
From playlist Intro to Linear Systems

Discrete-Time Dynamical Systems
This video shows how discrete-time dynamical systems may be induced from continuous-time systems. https://www.eigensteve.com/
From playlist Data-Driven Dynamical Systems

Linear Algebra - Lecture 10 - Homogeneous Linear Systems
In this lecture, we define "homogeneous" linear systems, and discuss how to find the solutions to these systems in parametric vector form.
From playlist Linear Algebra Lectures

System of Equations with Three Equations and Three Variables
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys System of Equations with Three Equations and Three Variables
From playlist Systems of Equations

Queue Data Structure – Algorithms
This is an explanation of the dynamic data structure known as a queue. It compares a linear queue implemented by means of a dynamic array with a linear queue implemented with a static array. It also includes an explanation of how a circular queue works, along with pseudocode for the enqu
From playlist Data Structures

Graphing the system of two linear inequalities with two horizontal line
👉 Learn how to graph a system of inequalities. A system of inequalities is a set of inequalities which are collectively satisfied by a certain range of values for the variables. To graph a system of inequalities, each inequality making up the system is graphed individually with the side of
From playlist Solve a System of Inequalities by Graphing
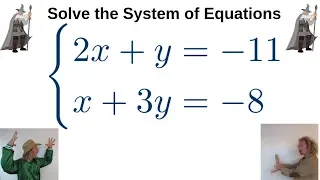
Systems of Equations with Substitution Two Variables Two Equations Example 1
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Systems of Equations with Substitution Two Variables Two Equations Example 1
From playlist Systems of Equations

How to solve a system of equations with three variables
👉Learn how to solve a system of three linear systems. A system of equations is a set of equations which are to be solved simultaneously. A linear equation is an equation whose graph is a straight line. The solution to a system of equations is a set of unique values of the variables for wh
From playlist 3 Examples: Solve a System of Three Equations

Policing London - The Thief-Taker General - Extra History - #1
Watch this video ad-free on Nebula: https://nebula.tv/videos/extra-history-policing-london-the-thief-taker-general-extra-history-1 These days we kind of assume that police are a normal part of law and order. But that wasn't always the case. In fact, it wasn't the case for a lot of human h
From playlist Extra History: Policing London

Solve a system with three variables
👉Learn how to solve a system of three linear systems. A system of equations is a set of equations which are to be solved simultaneously. A linear equation is an equation whose graph is a straight line. The solution to a system of equations is a set of unique values of the variables for wh
From playlist Solve a System of Equations With Three Variables

Vasily Pestun - 2/4 Quantum gauge theories and integrable systems
Seiberg-Witten theory maps supersymmetric four-dimensional gauge theories with extended supersymmetry to algebraic completely integrable systems. For large class of such integrable systems the phase space is the moduli space of solutions of self-dual hyperKahler equations and their low-dim
From playlist Vasily Pestun - Quantum gauge theories and integrable system

Vasily Pestun - 3/4 Quantum gauge theories and integrable systems
Seiberg-Witten theory maps supersymmetric four-dimensional gauge theories with extended supersymmetry to algebraic completely integrable systems. For large class of such integrable systems the phase space is the moduli space of solutions of self-dual hyperKahler equations and their low-dim
From playlist Vasily Pestun - Quantum gauge theories and integrable system

Vasily Pestun - 4/4 Quantum gauge theories and integrable systems
Seiberg-Witten theory maps supersymmetric four-dimensional gauge theories with extended supersymmetry to algebraic completely integrable systems. For large class of such integrable systems the phase space is the moduli space of solutions of self-dual hyperKahler equations and their low-dim
From playlist Vasily Pestun - Quantum gauge theories and integrable system

The Goldman symplectic form on the Hitchin component by Tengren Zhang
SURFACE GROUP REPRESENTATIONS AND GEOMETRIC STRUCTURES DATE: 27 November 2017 to 30 November 2017 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The focus of this discussion meeting will be geometric aspects of the representation spaces of surface groups into semi-simple Lie groups. Classi
From playlist Surface Group Representations and Geometric Structures

Higher solutions of Hitchin’s selfduality equations and real sections by Sebastian Heller
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

Introduction into spectral networks (Lecture 1) by Lotte Hollands
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

An invitation to higher Teichmüller theory – Anna Wienhard – ICM2018
Geometry Invited Lecture 5.11 An invitation to higher Teichmüller theory Anna Wienhard Abstract: Riemann surfaces are of fundamental importance in many areas of mathematics and theoretical physics. The study of the moduli space of Riemann surfaces of a fixed topological type is intimatel
From playlist Geometry

The Geometric Langlands conjecture and non-abelian Hodge theory (Lecture 2) by Ron Donagi
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

The Geometric Langlands conjecture and non-abelian Hodge theory (Lecture 3) by Ron Donagi
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Solving a system of three equations with infinite many solutions
👉Learn how to solve a system of three linear systems. A system of equations is a set of equations which are to be solved simultaneously. A linear equation is an equation whose graph is a straight line. The solution to a system of equations is a set of unique values of the variables for wh
From playlist Solve a System of Equations With Three Variables