
How to solve differentiable equations with logarithms
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Differential Equations
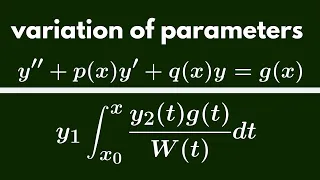
Differential Equations | Variation of Parameters.
We derive the general form for a solution to a differential equation using variation of parameters. http://www.michael-penn.net
From playlist Differential Equations
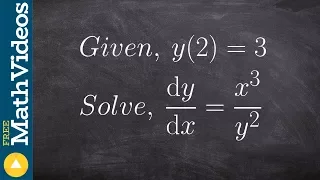
How to find the particular solution of a differential equation
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

How to solve a differentialble equation by separating the variables
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

Find the particular solution given the conditions and second derivative
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

Introduction to Differential Equations
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Differential Equations - The types of differential equations, ordinary versus partial. - How to find the order of a differential equation.
From playlist Differential Equations
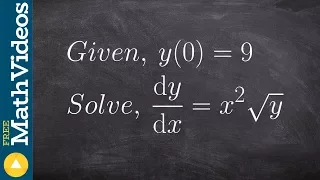
Solve the particular solution differentiable equations by separating the variables
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

How to solve a separable differential equation
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

C07 Homogeneous linear differential equations with constant coefficients
An explanation of the method that will be used to solve for higher-order, linear, homogeneous ODE's with constant coefficients. Using the auxiliary equation and its roots.
From playlist Differential Equations

Drawing Phase Portraits for Nonlinear Systems
This video shows how to draw phase portraits and analyze fully nonlinear systems. Specifically, we identify all of the fixed points, linearize around these fixed points, analyze the stability with eigenvalues and eigenvectors, and then infer global nonlinear dynamics outside of these regi
From playlist Engineering Math: Differential Equations and Dynamical Systems

MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015 View the complete course: http://ocw.mit.edu/10-34F15 Instructor: William Green Students learned numerical methods to solve ordinary differential equation with boundary value problems. License: Creative Commons BY-NC-
From playlist MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015

Mathematics for Machine Learning - Multivariate Calculus - Full Online Specialism
Welcome to the “Mathematics for Machine Learning: Multivariate Calculus” course, offered by Imperial College London. This video is an online specialisation in Mathematics for Machine Learning (m4ml) hosted by Coursera. For more information on the course and to access the full experience
From playlist Mathematics for Machine Learning - Multivariate Calculus

Transdifferentiation and oscillatory states in gene regulatory networks by Mithun Kumar Mitra
Indian Statistical Physics Community Meeting 2016 URL: https://www.icts.res.in/discussion_meeting/details/31/ DATES Friday 12 Feb, 2016 - Sunday 14 Feb, 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore This is an annual discussion meeting of the Indian statistical physics community wh
From playlist Indian Statistical Physics Community Meeting 2016

Semyon Dyatlov - Spectral gaps for normally hyperbolic trapping
Motivated by wave decay for Kerr and Kerr‐de Sitter black holes, we study spectral gaps for codimension 2 normally hyperbolic trapped sets with smooth stable/unstable foliations. Using semiclassical defect measures, we recover the gap of Wunsch‐Zworski and Nonnenmacher‐Zworski in our ca
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Einstein's General Theory of Relativity | Lecture 11
Lecture 11 of Leonard Susskind's Modern Physics concentrating on General Relativity. Recorded December 1, 2008 at Stanford University. This Stanford Continuing Studies course is the fourth of a six-qarter sequence of classes exploring the essential theoretical foundations of modern phys
From playlist Lecture Collection | Modern Physics: Einstein's Theory

Lec 8 | MIT 18.085 Computational Science and Engineering I
Applications to boundary value problems: Laplace equation A more recent version of this course is available at: http://ocw.mit.edu/18-085f08 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.085 Computational Science & Engineering I, Fall 2007

18. Electron Transport and Thermoelectric Effects
MIT 2.57 Nano-to-Micro Transport Processes, Spring 2012 View the complete course: http://ocw.mit.edu/2-57S12 Instructor: Gang Chen License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 2.57 Nano-to-Micro Transport Processes, Spring 2012

Introduction to State-Space Equations | State Space, Part 1
Check out the other videos in the series: https://youtube.com/playlist?list=PLn8PRpmsu08podBgFw66-IavqU2SqPg_w Part 2 - Pole placement: https://youtu.be/FXSpHy8LvmY Part 3 - Observability and Controllability: https://youtu.be/BYvTEfNAi38 Part 4 - What Is LQR Optimal Control: https://youtu
From playlist State Space

Solve differentiable equations with In
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Differential Equations

(March 11, 2013) Leonard Susskind presents the theory of cosmological inflation under which the early universe expanded exponentially before the Big Bang. This theory explains the lack of observed magnetic monopoles and the uniformity of the cosmic microwave background radiation. Origina
From playlist Lecture Collection | Cosmology