
First order sinusoidal response
The first part of understanding the frequency domain is understanding the effect of sinusoidal forcing
From playlist Frequency domain
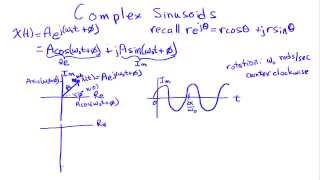
Basic decomposition of a complex sinusoid into a real part consisting of a cosine and an imaginary part consisting of a sine. http://AllSignalProcessing.com for free e-book on frequency in signal processing and much more.
From playlist Background Material

http://AllSignalProcessing.com for free e-book on frequency in signal processing and much more. Introduction to continuous- and discrete-time sinusoids, relationship between discrete- and continuous-time frequency through sampling, and illustration of using sinusoids to represent more com
From playlist Introduction and Background

Frequency Response Descriptions for LTI Systems
http://AllSignalProcessing.com for free e-book on frequency relationships and more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files. An introduction to the description of the input output characteristics of linear time-invariant systems b
From playlist Introduction and Background

Represent a Discrete Function Using Ordered Pairs, a Table, and Function Notation
This video explains how to represent a discrete function given as points as ordered pairs, a table, and using function notation. http://mathispower4u.com
From playlist Introduction to Functions: Function Basics

Ex: Determine Function Inputs and Outputs Given a Function as Ordered Pairs
This video provides examples of how to find function inputs and outputs when given a function as a set or points or ordered pairs. Site: http://mathispoweru4.com
From playlist Determining Function Values
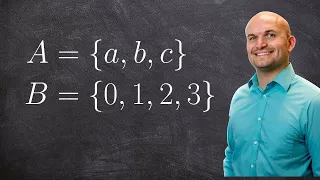
How to determine if an ordered pair is a function or not
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

Connecting Different Representations of Functions - Given Function Formula (L8.5)
This lesson makes the connection among various representations of a function including a table, a graph, a function rule, and a written description of a function. Content created by Jenifer Bohart and Amy Volpe from Scottsdale CC (License CC-BY-SA 4.0)
From playlist Introduction to Functions: Function Basics

Lec 22 | MIT 2.71 Optics, Spring 2009
Lecture 22: Coherent and incoherent imaging Instructor: George Barbastathis, Colin Sheppard, Se Baek Oh View the complete course: http://ocw.mit.edu/2-71S09 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 2.71 Optics, Spring 2009
EE102: Introduction to Signals & Systems, Lecture 14
These lectures are from the EE102, the Stanford course on signals and systems, taught by Stephen Boyd in the spring quarter of 1999. More information is available at https://web.stanford.edu/~boyd/ee102/
From playlist EE102: Introduction to Signals & Systems

How can the response of a system to sinusoidal inputs be useful? I explore the links between Fourier series and the Laplace transform in this video
From playlist Frequency domain
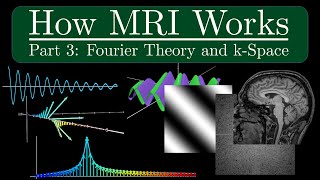
How MRI Works - Part 3 - Fourier Transform and K-Space
How MRI works, Part 3 - The Fourier Transform and k-Space Part 1: https://youtu.be/TQegSF4ZiIQ Part 2: https://youtu.be/M7yh0To6Wbs FFT code: https://github.com/thePIRL/fft-code-for-fun/blob/main/FFT%20code 0:00 - Intro 1:00 - The Sinusoid and phasors 5:48 - Fourier Theory 9:05 - The Fo
From playlist Summer of Math Exposition 2 videos

16. Describing Functions (continued)
MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

Extremum Seeking Control in Matlab
This lecture explores extremum-seeking control (ESC) on a simple example in Matlab. In particular, a discrete-time (digital) version of ESC is coded in a Matlab script. Real-Time Optimization by Extremum-Seeking Control K. B. Ariyur and M. Krstić, Wiley 2003. https://onlinelibrary.wile
From playlist Data-Driven Control with Machine Learning

MIT Electronic Feedback Systems (1985) View the complete course: http://ocw.mit.edu/RES6-010S13 Instructor: James K. Roberge License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Electronic Feedback Systems (1985)

Injective, Surjective and Bijective Functions (continued)
This video is the second part of an introduction to the basic concepts of functions. It looks at the different ways of representing injective, surjective and bijective functions. Along the way I describe a neat way to arrive at the graphical representation of a function.
From playlist Foundational Math

EE102: Introduction to Signals & Systems, Lecture 4
These lectures are from the EE102, the Stanford course on signals and systems, taught by Stephen Boyd in the spring quarter of 1999. More information is available at https://web.stanford.edu/~boyd/ee102/
From playlist EE102: Introduction to Signals & Systems
