Lesson 22: Deep Learning Foundations to Stable Diffusion
Oops I say it's "Lesson 21" at the start of the video -- but actually this is lesson 22! (All lesson resources are available at http://course.fast.ai.) Jeremy begins this lesson with a discussion of improvements to the DDPM/DDIM implementation. He explores the removal of the concept of an
From playlist Practical Deep Learning 2022 Part 2

(New Version Available) Inverse Functions
New Version: https://youtu.be/q6y0ToEhT1E Define an inverse function. Determine if a function as an inverse function. Determine inverse functions. http://mathispower4u.wordpress.com/
From playlist Exponential and Logarithmic Expressions and Equations

Holger Dullin: The Lagrange top and the confluent Heun equation
Abstract: The Lagrange Top (heavy symmetric rigid body with a fixed point) with an additional quadratic potential is described in global coordinates using a 7-dimensional Poisson structure. The set of critical values of the energy-momentum map has a rational parametrisation that is derived
From playlist Integrable Systems 9th Workshop

ch9 5. Runge-Kutta Methods. Euler step and Heun step. Wen Shen
Wen Shen, Penn State University. Lectures are based on my book: "An Introduction to Numerical Computation", published by World Scientific, 2016. See promo video: https://youtu.be/MgS33HcgA_I
From playlist CMPSC/MATH 451 Videos. Wen Shen, Penn State University

Computational Physics Lecture 22, Numerical Integration of ODEs
In this lecture, we introduce the basic methods for solving ordinary differential equations. We discuss the Euler's method, Heun's method, and the midpoint method. This video was created to accompany the course "Computational Physics (PHYS 270)" taught in the spring of 2017 at Nazarbayev
From playlist Nazarbayev: PHYS 270 - Computational Physics with Ernazar Ab

New in Fractional Differentiation
In the scientific literature, one sees a lot of approaches to fractional order integro-differentiation. In this talk, we present numerous essential details of the most natural Riemann–Liouville–Hadamard construction for fractional differentiation, which has been published in the Wolfram Fu
From playlist Wolfram Technology Conference 2021
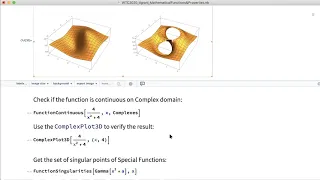
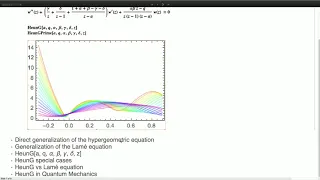
Mathematical Functions and Properties
The Wolfram Language has over 250 mathematical functions, including well-known elementary and special functions that have played a crucial role in the development of science for decades. Although this set is almost complete, we are continuously implementing new functionality for mathematic
From playlist Wolfram Technology Conference 2020

Diagonals of Rational Functions Diagonals of rational functions naturally occur in many applications, study several families of rational functions in three or four variables and investigate the nature of their diagonals (hypergeometric 2F1 functions, Heun functions, modular forms, functi
From playlist DART X

Define an inverse function. Determine if a function as an inverse function. Determine inverse functions.
From playlist Determining Inverse Functions
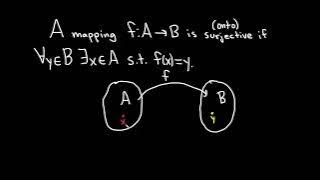
Definition of a Surjective Function and a Function that is NOT Surjective
We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht
From playlist Injective, Surjective, and Bijective Functions

Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions
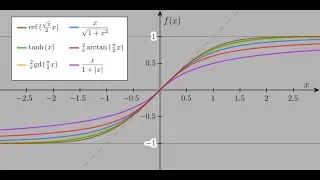
Sigmoid functions for population growth and A.I.
Some elaborations on sigmoid functions. https://en.wikipedia.org/wiki/Sigmoid_function https://www.learnopencv.com/understanding-activation-functions-in-deep-learning/ If you have any questions of want to contribute to code or videos, feel free to write me a message on youtube or get my co
From playlist Analysis

What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions

Working with Functions (1 of 2: Notation & Terminology)
More resources available at www.misterwootube.com
From playlist Working with Functions

Functions of equations - IS IT A FUNCTION
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function
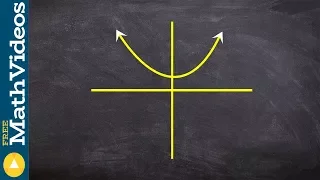
Using the vertical line test to determine if a graph is a function or not
👉 Learn how to determine whether relations such as equations, graphs, ordered pairs, mapping and tables represent a function. A function is defined as a rule which assigns an input to a unique output. Hence, one major requirement of a function is that the function yields one and only one r
From playlist What is the Domain and Range of the Function

Lilya Budaghyan : On APN and AB power functions
CONFERENCE Recording during the thematic meeting : « ALgebraic and combinatorial methods for COding and CRYPTography» the February 23, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given b
From playlist Combinatorics

Kotlin Functions Tutorial | Kotlin Functional Programming Explained | Kotlin Tutorial | Simplilearn
🔥Post Graduate Program In Full Stack Web Development: https://www.simplilearn.com/pgp-full-stack-web-development-certification-training-course?utm_campaign=KotlinFunctionsTutorial-obN78NEd47g&utm_medium=DescriptionFF&utm_source=youtube 🔥Caltech Coding Bootcamp (US Only): https://www.simpli
From playlist C++ Tutorial Videos