Heat capacity ratio

Ratios

In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure (CP) to heat capacity at constant volume (CV). It is sometimes also known as the isentropic expansion factor and is denoted by γ (gamma) for an ideal gas or κ (kappa), the isentropic exponent for a real gas. The symbol γ is used by aerospace and chemical engineers. where C is the heat capacity, the molar heat capacity (heat capacity per mole), and c the specific heat capacity (heat capacity per unit mass) of a gas. The suffixes P and V refer to constant-pressure and constant-volume conditions respectively. The heat capacity ratio is important for its applications in thermodynamical reversible processes, especially involving ideal gases; the speed of sound depends on this factor. To understand this relation, consider the following thought experiment. A closed pneumatic cylinder contains air. The piston is locked. The pressure inside is equal to atmospheric pressure. This cylinder is heated to a certain target temperature. Since the piston cannot move, the volume is constant. The temperature and pressure will rise. When the target temperature is reached, the heating is stopped. The amount of energy added equals CV ΔT, with ΔT representing the change in temperature. The piston is now freed and moves outwards, stopping as the pressure inside the chamber reaches atmospheric pressure. We assume the expansion occurs without exchange of heat (adiabatic expansion). Doing this work, air inside the cylinder will cool to below the target temperature. To return to the target temperature (still with a free piston), the air must be heated, but is no longer under constant volume, since the piston is free to move as the gas is reheated. This extra heat amounts to about 40% more than the previous amount added. In this example, the amount of heat added with a locked piston is proportional to CV, whereas the total amount of heat added is proportional to CP. Therefore, the heat capacity ratio in this example is 1.4. Another way of understanding the difference between CP and CV is that CP applies if work is done to the system, which causes a change in volume (such as by moving a piston so as to compress the contents of a cylinder), or if work is done by the system, which changes its temperature (such as heating the gas in a cylinder to cause a piston to move). CV applies only if , that is, no work is done. Consider the difference between adding heat to the gas with a locked piston and adding heat with a piston free to move, so that pressure remains constant. In the second case, the gas will both heat and expand, causing the piston to do mechanical work on the atmosphere. The heat that is added to the gas goes only partly into heating the gas, while the rest is transformed into the mechanical work performed by the piston. In the first, constant-volume case (locked piston), there is no external motion, and thus no mechanical work is done on the atmosphere; CV is used. In the second case, additional work is done as the volume changes, so the amount of heat required to raise the gas temperature (the specific heat capacity) is higher for this constant-pressure case. (Wikipedia).

Specific heat capacity explained, measured and demonstrated: by fizzics.org

Specific heat capacity of a material is the quantity which describes how much energy is required to raise the temperature. The lesson demonstrates the amount of energy supplied to heat water and the specific heat capacity of the water is measured with a calculation. Notes on specific heat

From playlist Thermal energy/heat

What Is The Difference Between Specific Heat Capacity, Heat Capacity, and Molar Heat Capacity

This chemistry video tutorial explains the difference between specific heat capacity, heat capacity, and molar heat capacity. It contains a few examples and practice problems on calculating the specific heat capacity and molar heat capacity of a substance. It provides all of the equation

From playlist New AP & General Chemistry Video Playlist

Heat capacity

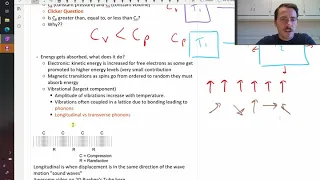
An important thermal property is heat capacity which is the amount of energy that gets absorbed to make some quantity of material increase 1 degree in temperature. This can be per mole or per mass (specific heat capacity). Heat capacity increases until the Dulong-Petit limit of 3R above th

From playlist Materials Sciences 101 - Introduction to Materials Science & Engineering 2020

Specific Heat Capacity | Matter | Physics | FuseSchool

Specific Heat Capacity | Matter | Physics | FuseSchool You might have noticed that if you are trying to boil a lot of water it takes longer than if you only wish to boil a small amount of water. This is all because of something called ‘heat capacity’. Keep watching to learn more. Befo

From playlist PHYSICS

Physics - Thermodynamics: (3 of 22) Molar Heat Capacity Of A Gas

Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the molar heat capacity of a gas.

From playlist PHYSICS - THERMODYNAMICS

Physics - Thermodynamics: (6 of 14) Efficiency of a Heat Engine: Example 2

Visit http://ilectureonline.com for more math and science lectures! In this video I will show you how to calculate the efficiency of an (heat) engine, example 2.

From playlist PHYSICS - THERMODYNAMICS

Chemistry - Liquids and Solids (16 of 59) Structures & Properties of H2O: High Heat Capacity

Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the structures and properties of water (high heat capacity).

From playlist CHEMISTRY 16 LIQUIDS AND SOLIDS

Specific Heat Capacity Problems & Calculations - Chemistry Tutorial - Calorimetry

This chemistry video tutorial explains the concept of specific heat capacity and it shows you how to use the formula to solve specific heat capacity problems. This video contains plenty of examples, notes, and practice problems with the calculations to help you master this topic. My E-B

From playlist New Physics Video Playlist

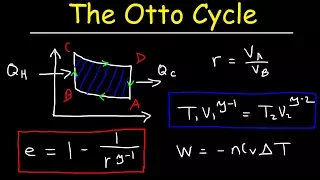
Otto Cycle of Internal Combustion Engines, Gamma vs Compression Ratio, Adiabatic Processes - Physics

This physics video tutorial provides a basic introduction into the otto cycle of an internal combustion engine. The first step is an adiabatic process when the gas undergoes compression. As the volume decreases, the temperature of the gas increases and the pressure greatly increases favo

From playlist New Physics Video Playlist

Internal Energy of an Ideal Gas - Molar Heat Capacity of Monatomic & Diatomic Gases, Gamma Ratio,

This physics video tutorial explains how to calculate the internal energy of an ideal gas - this includes monatomic gases and diatomic gases. You need to know how to calculate the molar heat capacity of a gas especially if you're given the gamma ratio of a gas. This thermodynamics video

From playlist New Physics Video Playlist

Thermodynamics 1b - Heat and Temperature II

Here we complete our discussion of the concepts of heat and temperature.

From playlist Thermodynamics

Thermodynamics: Specific Heat Capacity Calculations

This video explains how to calculate the change in heat, the change in temperature and the specific heat of a substance. The change in heat is calculated as the mass of the substance times the specific heat of the substance times the change in temperature of the substance. Q = m x c x T

From playlist Thermal Physics/Fluid Mechanics

Field Induced Quantum Phase Transitions in one-Dimensional Spin...by Ramesh Chandra Nath

PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In

From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)

Carnot Heat Engines, Efficiency, Refrigerators, Pumps, Entropy, Thermodynamics - Second Law, Physics

This physics tutorial video shows you how to solve problems associated with heat engines, carnot engines, efficiency, work, heat, refrigerators, heat pumps and entropy. It discusses the concepts of the first and second law of thermodynamics. This video contains plenty of examples and pra

From playlist New Physics Video Playlist

Thermodynamics and Chemical Dynamics 131C. Lecture 13. The Carnot Cycle.

UCI Chem 131C Thermodynamics and Chemical Dynamics (Spring 2012) Lec 13. Thermodynamics and Chemical Dynamics -- The Carnot Cycle -- View the complete course: http://ocw.uci.edu/courses/chem_131c_thermodynamics_and_chemical_dynamics.html Instructor: Reginald Penner, Ph.D. License: Creati

From playlist Chemistry 131C: Thermodynamics and Chemical Dynamics

Mod-01 Lec-11 Thermal Conductivity of Metals

Condensed Matter Physics by Prof. G. Rangarajan, Department of Physics, IIT Madras. For more details on NPTEL visit http://nptel.iitm.ac.in

From playlist NPTEL: Condensed Matter Physics - CosmoLearning.com Physics Course

Shannon 100 - 28/10/2016 - Ruediger URBANK

Happy Numbers: 68 Years of Coding, 6² + 8² = 100 Years of Shannon, 1² + 0² + 0² = 1 Goal Ruediger Urbank (EPFL) This year, we celebrate Shannon’s 100th birthday and it has been 68 years since he laid the foundations of communications. To realize his number 1 goal or error free communica

From playlist Shannon 100

feb10

mse 3310 spring 2017

From playlist Introduction to Ceramics Spring 2017

W#20 Specific heat capacity

Preliminary Chemistry Water Specific heat capacity

From playlist Preliminary Chemistry - Water

Heat capacity ratio

Related pages