
Powered by https://www.numerise.com/ Equation of a circle 3
From playlist Coordinate geometry of a circle

Why the unit circle is so helpful for us to evaluate trig functions
👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Trigonometric Functions and The Unit Circle

How to memorize the unit circle
👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Learn how to construct the unit circle
👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

How to find the point on the unit circle from the given real number
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

How to find a point on the unit circle given an angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Paul Melotti - Récurrence spatiales, modèles associés et leurs formes limites
Certaines relations polynomiales, telles que les relations vérifiées par les mineurs d'une matrice, peuvent être interprétées comme des relations de récurrence sur Z^3. Dans certains cas, les solutions de ces récurrences présentent une propriété inattendue : ce sont des polynômes de Lauren
From playlist Les probabilités de demain 2017

Finding and Solving the Hadamard Population Conjecture
We describe our process for finding and solving the Hadamard Population conjecture. This conjecture is for all v, for all w, fht(v) dot-product fht(w) = n * population(v intersect w), where v and w are binary vectors and n is the length of all vectors. This is a submission to the #SoME2 co
From playlist Summer of Math Exposition 2 videos
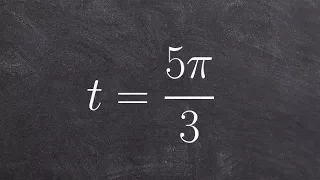
How to determine the point on the unit circle given an angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Christian Bär: Local index theory for Lorentzian manifolds
HYBRID EVENT We prove a local version of the index theorem for Dirac-type operators on globally hyperbolic Lorentzian manifolds with Cauchy boundary. In case the Cauchy hypersurface is compact, we do not assume self-adjointness of the Dirac operator on the spacetime or of the associated el
From playlist Mathematical Physics

Learning to determine the point on the unit circle by sketching the angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
Thomas Weighill - Coarse homotopy groups of warped cones
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Thomas Weighill, University of North Carolina at Greensboro Title: Coarse homotopy groups of warped cones Abstract: Various versions of coarse homotopy theory have been around since the beginning of coarse geometry, and s
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Complex Analysis (Advanced) -- The Schwarz Lemma
A talk I gave concerning my recent results on the Schwarz Lemma in Kähler and non-Kähler geometry. The talk details the classical Schwarz Lemma and discusses André Bloch. This is part 1 of a multi-part series. Part 1 -- https://youtu.be/AWqeIPMNhoA Part 2 -- https://youtu.be/hd7-iio77kc P
From playlist Complex Analysis

Number theoretic aspects of multiplicative chaos - Adam Harper
50 Years of Number Theory and Random Matrix Theory Conference Topic: Number theoretic aspects of multiplicative chaos Speaker: Adam Harper Affiliation: University of Warwick Date: June 22, 2022 Multiplicative chaos is the general name for a family of probabilistic objects, which can be t
From playlist Mathematics

Quantum computation (Lecture 02) by Peter Young
ORGANIZERS : Abhishek Dhar and Sanjib Sabhapandit DATE : 27 June 2018 to 13 July 2018 VENUE : Ramanujan Lecture Hall, ICTS Bangalore This advanced level school is the ninth in the series. This is a pedagogical school, aimed at bridging the gap between masters-level courses and topics
From playlist Bangalore School on Statistical Physics - IX (2018)

Complex Analysis - Part 9 - Power Series
Support the channel on Steady: https://steadyhq.com/en/brightsideofmaths Or support me via PayPal: https://paypal.me/brightmaths Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics Or via Patreon: https://www.patreon.com/bsom Or via other methods: https://thebrightsideofmathematics.
From playlist Complex Analysis

Spacetime Singularities - Roger Penrose, Dennis Lehmkuhl and Melvyn Bragg
All aboard the Oxford Mathematics Space Probe for this Public Lecture as we explore Black Holes with a Nobel Laureate, a Professor of the History and Philosophy of Physics & a broadcasting legend. Even Albert Einstein had thought Black Holes impossible. Then in 1965 Roger Penrose provide
From playlist The Roger Penrose Playlist

👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
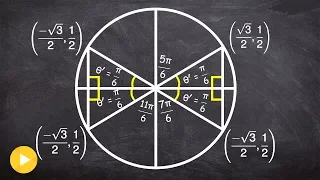
Quickly fill in the unit circle by understanding reference angles and quadrants
👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Trigonometric Functions and The Unit Circle

Anne Broadbent - Information-Theoretic Quantum Cryptography Part 1 of 2 - IPAM at UCLA
Recorded 27 July 2022. Anne Broadbent of the University of Ottawa presents "Information-Theoretic Quantum Cryptography" at IPAM's Graduate Summer School Post-quantum and Quantum Cryptography. Abstract: These lectures are an introduction to the interplay between quantum information and cryp
From playlist 2022 Graduate Summer School on Post-quantum and Quantum Cryptography