
(PP 6.1) Multivariate Gaussian - definition
Introduction to the multivariate Gaussian (or multivariate Normal) distribution.
From playlist Probability Theory

What is a Sampling Distribution?
Intro to sampling distributions. What is a sampling distribution? What is the mean of the sampling distribution of the mean? Check out my e-book, Sampling in Statistics, which covers everything you need to know to find samples with more than 20 different techniques: https://prof-essa.creat
From playlist Probability Distributions

This lesson introduces the different sample methods when conducting a poll or survey. Site: http://mathispower4u.com
From playlist Introduction to Statistics

What is purposive (deliberate) sampling? Types of purposive sampling, advantages and disadvantages. Check out my e-book, Sampling in Statistics, which covers everything you need to know to find samples with more than 20 different techniques: https://prof-essa.creator-spring.com/listing/sam
From playlist Sampling

(ML 16.7) EM for the Gaussian mixture model (part 1)
Applying EM (Expectation-Maximization) to estimate the parameters of a Gaussian mixture model. Here we use the alternate formulation presented for (unconstrained) exponential families.
From playlist Machine Learning

Overview of non probability sampling; advantages and disadvantages, types. Check out my e-book, Sampling in Statistics, which covers everything you need to know to find samples with more than 20 different techniques: https://prof-essa.creator-spring.com/listing/sampling-in-statistics
From playlist Sampling
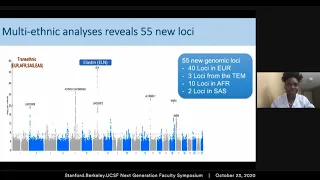
Multi-ethnic GWAS study of aorta diameter and polygenic risk prediction for thoracic aortic disease
Dr. Catherine Tcheandjieu, Stanford University 2020 Stanford.Berkeley.UCSF Next Generation Faculty Symposium
From playlist 2020 Stanford.Berkeley.UCSF Next Generation Faculty Symposium

The Power of Sampling by Peter W. Glynn
Infosys-ICTS Turing Lectures The Power of Sampling Speaker: Peter W. Glynn (Stanford University, USA) Date: 14 August 2019, 16:00 to 17:00 Venue: Ramanujan Lecture Hall, ICTS Bangalore Sampling-based methods arise in many statistical, computational, and engineering settings. In engine
From playlist Infosys-ICTS Turing Lectures

Anup Rao : Communication Complexity and Information Complexity - 4
The study of efficient communication communication using tools from information theory has led to many interesting results for basic problems in the last few decades. In this mini-course, we shall learn the basic concepts of communication complexity and see some its applications to distrib
From playlist Nexus Trimester - 2016 -Tutorial Week at CIRM

Perception, Action, and Experience: Retying the Golden Braid
Intuitively, our mental life involves, as Andy Clark evocatively puts it, “a seamless unfolding of perception, action and experience: a golden braid in which each element twines intimately with the rest.” Cognitive science is widely held to have decisively unraveled these strands, inspirin
From playlist Whitney Humanities Center

An overview and introduction to understanding sampling distributions of proportions [sample proportions] and how to calculate them
From playlist Unit 7 Probability C: Sampling Distributions & Simulation

JUDGMENT and SNOWBALL Non-random Sampling (12-6)
Judgment sampling (a.k.a., expert sampling, authoritative sampling, purposive sampling, judgmental sampling) is a technique in which the sample is selected based on the researcher’s (or other experts’) existing knowledge or professional judgment. It may provide highly accurate findings wit
From playlist Sampling Distributions in Statistics (WK 12 - QBA 237)

Jennifer Listgarten: "Structured Populations in Genetics"
Computational Genomics Summer Institute 2016 "Structured Populations in Genetics" Jennifer Listgarten, Microsoft Research Institute for Pure and Applied Mathematics, UCLA July 21, 2016 For more information: http://computationalgenomics.bioinformatics.ucla.edu/
From playlist Computational Genomics Summer Institute 2016

05c Data Analytics: Distribution Transform
A short discussion on the topic of distribution transforms, e.g. transforming your data to the parametric Gaussian distribution.
From playlist Data Analytics and Geostatistics

Distinguished Visitor Lecture by Xihong Lin Scalable Analysis of Large Multi Ethic Biobanks and ...
Scalable Analysis of Large Multi Ethic Biobanks and Whole Genome Sequencing Studies Xihong Lin Harvard University, USA
From playlist Distinguished Visitors Lecture Series

Bruno Klingler - 3/4 Tame Geometry and Hodge Theory
Hodge theory, as developed by Deligne and Griffiths, is the main tool for analyzing the geometry and arithmetic of complex algebraic varieties. It is an essential fact that at heart, Hodge theory is NOT algebraic. On the other hand, according to both the Hodge conjecture and the Grothendie
From playlist Bruno Klingler - Tame Geometry and Hodge Theory

Invariant Measures for Non-autonomous systems.... by Sergey Kryzhevich
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

filter / edges - CS50 Walkthroughs 2019
*** This is CS50, Harvard University's introduction to the intellectual enterprises of computer science and the art of programming. *** HOW TO SUBSCRIBE http://www.youtube.com/subscription_center?add_user=cs50tv HOW TO TAKE CS50 edX: https://cs50.edx.org/ Harvard Extension School: ht
From playlist CS50 Walkthroughs 2019

C. Soulé - Arithmetic Intersection (Part4)
Let X be a 2-dimensional, normal, flat, proper scheme over the integers. Assume ¯L and ¯M are two hermitian line bundles over X. Arakelov (and Deligne) defined a real number ¯L.¯M, the arithmetic intersection number of ¯L and ¯M. We shall explain the definition and the basic properties of
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

Sampling Distributions and Confidence Intervals (Part 1 of Intro to Statistics)
Intro to Statistics Part 1. This is part one of a short course on foundations of statistics. If you've never taken a statistics class before (or even if you have), this course will walk you through what you need to know. Check out my e-book, Sampling in Statistics, which covers everythin
From playlist Intro to Statistics