
Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra
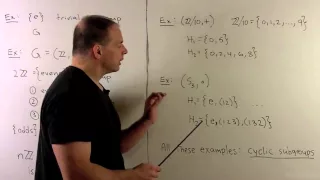
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)

Abstract Algebra: We introduce the notion of a group and describe basic properties. Examples given include familiar abelian groups and the symmetric groups. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-theory Master list at http://mathdoctorbob.o
From playlist Abstract Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

Center of a group in abstract algebra
After the previous video where we saw that two of the elements in the dihedral group in six elements commute with all the elements in the group, we finally get to define the center of a group. The center of a group is a subgroup and in this video we also go through the proof to show this.
From playlist Abstract algebra

Benjamin Steinberg: Cartan pairs of algebras
Talk by Benjamin Steinberg in Global Noncommutative Geometry Seminar (Americas), https://globalncgseminar.org/talks/tba-15/ on Oct. 8, 2021
From playlist Global Noncommutative Geometry Seminar (Americas)

Erik van Erp: Lie groupoids in index theory 4
The lecture was held within the framework of the Hausdorff Trimester Program Non-commutative Geometry and its Applications. 12.9.2014
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Erik van Erp: Pseudodifferential Calculi and Groupoids
In recent work Debord and Skandalis realized pseudodifferential operators (on an arbitrary Lie groupoid G) as integrals of certain smooth kernels on the adiabatic groupoid of G. We propose an alternative definition of pseudodifferential calculi (including nonstandard calculi like the Heise
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Abstract Algebra | Definition of a Group and Basic Examples
We present the definition of a group and give a few basic example s of abelian groups. http://www.michael-penn.net
From playlist Abstract Algebra

Tristan Bice, Dauns-Hofmann-Kumjian-Renault Duality for Fell Bundles and Structured C*-Algebras
Noncommutative Geometry Seminar(Asia-Pacific), Sep. 27, 2021
From playlist Global Noncommutative Geometry Seminar (Asia and Pacific)

Anna Duwenig: Non-commutative Poincaré duality of the irrational rotation algebra
Talk by Anna Duwenig in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on September 9, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Groups in abstract algebra examples
In this tutorial I discuss two more examples of groups. The first contains four elements and they are the four fourth roots of 1. The second contains only three elements and they are the three cube roots of 1. Under the binary operation of multiplication, these sets are in fact groups.
From playlist Abstract algebra

Tristan Bice, Dauns-Hofmann-Kumjian-Renault Duality for Fell Bundles and Structured C*-Algebras
Global Noncommutative Geometry Seminar(Asia-Pacific), Sep. 27, 2021
From playlist Global Noncommutative Geometry Seminar (Asia and Pacific)

Markus Pflaum: The transverse index theorem for proper cocompact actions of Lie groupoids
The talk is based on joint work with H. Posthuma and X. Tang. We consider a proper cocompact action of a Lie groupoid and define a higher index pairing between invariant elliptic differential operators and smooth groupoid cohomology classes. We prove a cohomological index formula for this
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Paulo Carrillo Rouse: Chern assembly map for discrete groups and index theory
Talk by Paulo Carrillo Rouse in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on April 14, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)
Structures in the Floer theory of Symplectic Lie Groupoids - James Pascaleff
Symplectic Dynamics/Geometry Seminar Topic: Structures in the Floer theory of Symplectic Lie Groupoids Speaker: James Pascaleff Affiliation: University of Illinois, Urbana-Champaign Date: October 15, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Abstract Algebra: Group actions are defined as a formal mechanism that describes symmetries of a set X. A given group action defines an equivalence relation, which in turn yields a partition of X into orbits. Orbits are also described as cosets of the group. U.Reddit course materials a
From playlist Abstract Algebra
