
I define topological manifolds. Motivated by the prospect of calculus on topological manifolds, I introduce smooth manifolds. At the end I point out how one needs to change the definitions, to obtain C^1 or even complex manifolds. To learn more about manifolds, see Lee's "Introduction to
From playlist Differential geometry

What is a Manifold? Lesson 2: Elementary Definitions
This lesson covers the basic definitions used in topology to describe subsets of topological spaces.
From playlist What is a Manifold?

What is a Manifold? Lesson 6: Topological Manifolds
Topological manifolds! Finally! I had two false starts with this lesson, but now it is fine, I think.
From playlist What is a Manifold?

What is a Manifold? Lesson 12: Fiber Bundles - Formal Description
This is a long lesson, but it is not full of rigorous proofs, it is just a formal definition. Please let me know where the exposition is unclear. I din't quite get through the idea of the structure group of a fiber bundle fully, but I introduced it. The examples in the next lesson will h
From playlist What is a Manifold?

Manifolds #5: Tangent Space (part 1)
Today, we introduce the notion of tangent vectors and the tangent vector space at a point on a manifold.
From playlist Manifolds
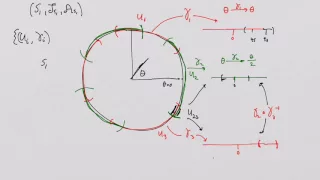
What is a Manifold? Lesson 13: The tangent bundle - an illustration.
What is a Manifold? Lesson 13: The tangent bundle - an illustration. Here we have a close look at a complete example using the tangent bundle of the manifold S_1. Next lesson we look at the Mobius strip as a fiber bundle.
From playlist What is a Manifold?
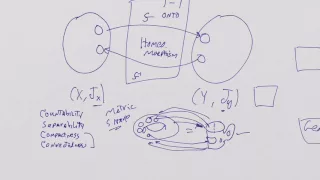
What is a Manifold? Lesson 5: Compactness, Connectedness, and Topological Properties
The last lesson covering the topological prep-work required before we begin the discussion of manifolds. Topics covered: compactness, connectedness, and the relationship between homeomorphisms and topological properties.
From playlist What is a Manifold?

Alberto Cattaneo: An introduction to the BV-BFV Formalism
Abstract: The BV-BFV formalism unifies the BV formalism (which deals with the problem of fixing the gauge of field theories on closed manifolds) with the BFV formalism (which yields a cohomological resolution of the reduced phase space of a classical field theory). I will explain how this
From playlist Topology

Ed Witten -- From Gauge Theory to Khovanov Homology Via Floer Theory
Edward Witten lecture entitled "From Gauge Theory to Khovanov Homology Via Floer Theory" as part of the Banff International Research Station conference "Perspectives on Knot Homology". The Banff International Research Station will host the "Perspectives on Knot Homology" workshop in Banf
From playlist Research Lectures

Eckhard Meinrenken: Differential Geometry of Weightings
Talk by Eckhard Meinrenken in Global Noncommutative Geometry Seminar (Americas) https://globalncgseminar.org/talks/differential_geometry_of_weightings/ on February 19, 2021.
From playlist Global Noncommutative Geometry Seminar (Americas)

Winter School JTP: Introduction to Fukaya categories, James Pascaleff, Lecture 3
This minicourse will provide an introduction to Fukaya categories. I will assume that participants are also attending Keller’s course on A∞ categories. Lecture 1: Basics of symplectic geometry for Fukaya categories. Symplectic manifolds; Lagrangian submanifolds; exactness conditions;
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Classification of n-component links with Khovanov homology of rank 2^n - Boyu Zhang
Symplectic Dynamics/Geometry Seminar Topic: Classification of n-component links with Khovanov homology of rank 2^n Speaker: Boyu Zhang Affiliation: Princeton University Date: February 24, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Knot surgery and Heegaard Floer homology - Jennifer Hom
Members' Seminar Topic: Knot surgery and Heegaard Floer homology Speaker: Jennifer Hom Date: Monday, April 4 One way to construct new 3-manifolds is by surgery on a knot in the 3-sphere; that is, we remove a neighborhood of a knot, and reglue it in a different way. What 3-manifolds ca
From playlist Mathematics

Manifolds 1.2 : Examples of Manifolds
In this video, I describe basic examples of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/IZO0G25
From playlist Manifolds

Tobias EKHOLM - 1/3 Introduction to knot contact homology
We define knot contact homology as the Legendrian differential graded algebra of the unit conormal lift of a knot. We show how to compute it for knots in the three sphere using flow trees and discuss some of its basic properties. We also introduce the augmentation variety. 13 juillet 2015
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

Allison Moore - Essential Conway spheres and Floer homology via immersed curves
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Allison Moore, Virginia Commonwealth University Title: Essential Conway spheres and Floer homology via immersed curves Abstract: We consider the problem of whether Dehn surgery along a knot in the three-sphere produces an
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Ian Zemke - Concordance surgery and the Ozsváth--Szabó 4-manifold invariant
June 29, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry II
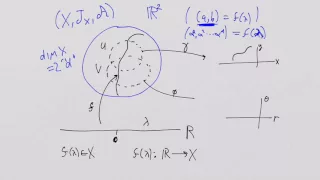
What is a Manifold? Lesson 8: Diffeomorphisms
What is a Manifold? Lesson 8: Diffeomorphisms
From playlist What is a Manifold?

Dichotomy & Poincare Duality by Somnath Basu
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)
