
The Computational Complexity of Geometric Topology Problems - Greg Kuperberg
Greg Kuperberg University of California, Davis September 24, 2012 This talk will be a partial survey of the first questions in the complexity theory of geometric topology problems. What is the complexity, or what are known complexity bounds, for distinguishing n-manifolds for various n? Fo
From playlist Mathematics

Geometric complexity theory from a combinatorial viewpoint - Greta Panova
Computer Science/Discrete Mathematics Seminar II Topic: Lattices: from geometry to cryptography Speaker: Greta Panova Affiliation: University of Pennsylvania; von Neumann Fellow, School of Mathematics Date: November 28, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

The geometric series.
From playlist Advanced Calculus / Multivariable Calculus

Learn about the geometric mean of numbers. The geometric mean of n numbers is the nth root of the product of the numbers. To find the geometric mean of n numbers, we first multiply the numbers and then take the nth root of the product.
From playlist Geometry - GEOMETRIC MEAN

Self Similar Geometric Series: Sums of powers of 7 (and all integers larger than 3)
This is a short, animated visual proof demonstrating the finite geometric sum formula for any integer n with n greater than 3 (explicitly showing the cases n=7 and n=9 with k=3). This series (and its infinite analog when x less than 1) is important for many results in calculus, discrete ma
From playlist Finite Sums

Introduction to Geometric Power Series
Introduction to Geometric Power Series If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Larson Calculus 9.9 Representation of Functions by Power Series

Results and open problems in theory of quantum complexity - Anindya De
Andris Ambainis University of Latvia; Member, School of Mathematics April 22, 2014 I will survey recent results and open problems in several areas of quantum complexity theory, with emphasis on open problems which can be phrased in terms of classical complexity theory or mathematics but ha
From playlist Mathematics

Learn how to determine the sum of a geometric finite series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series
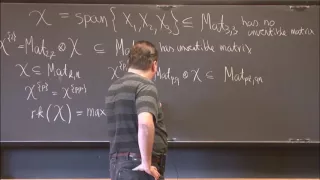
Matrix invariants and algebraic complexity theory - Harm Derksen
Computer Science/Discrete Mathematics Seminar I Topic: Matrix invariants and algebraic complexity theory Speaker: Harm Derksen More videos on http://video.ias.edu
From playlist Mathematics

Gauge Theory and the Analytic Approach to Geometric Langlands - Edward Witten
Clay Research Conference Topic: Gauge Theory and the Analytic Approach to Geometric Langlands Speaker: Edward Witten Affiliation: Professor, School of Natural Sciences Date: September 30, 2021 Recently P. Etingof, E. Frenkel, and D. Kazhdan, following earlier contributions by R. Langl
From playlist Mathematics

Quantization By Branes And Geometric Langlands Lecture 2 by Edward Witten
PROGRAM : QUANTUM FIELDS, GEOMETRY AND REPRESENTATION THEORY 2021 (ONLINE) ORGANIZERS : Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pan
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Quantization, Gauge Theory, And The Analytic Approach To Geometric... (Lecture 1) by Edward Witten
PROGRAM : QUANTUM FIELDS, GEOMETRY AND REPRESENTATION THEORY 2021 (ONLINE) ORGANIZERS : Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pan
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Edward Witten: Mirror Symmetry & Geometric Langlands [2012]
2012 FIELDS MEDAL SYMPOSIUM Thursday, October 18 Geometric Langlands Program and Mathematical Physics 1.30am-2.30pm Edward Witten, Institute for Advanced Study, Princeton "Superconformal Field Theory And The Universal Kernel of Geometric Langlands" The universal kernel of geometric Langl
From playlist Number Theory

Minerva Lectures 2012 - Ian Agol Talk 2: The virtual Haken conjecture & geometric group theory
Talk two of the second Minerva lecture series, by Prof. Ian Agol on October 23rd, 2012 at the Mathematics Department, Princeton University. More information available at: http://www.math.princeton.edu/events/seminars/minerva-lectures/minerva-lecture-ii-virtual-haken-conjecture-what-geomet
From playlist Minerva Lectures - Ian Agol

Lecture 1: Geometric Langlands and S-duality in N = 4 SYM by Sergei Gukov
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Jens Eberhardt: Motivic Springer Theory
27 September 2021 Abstract: Algebras and their representations can often be constructed geometrically in terms of convolution of cycles. For example, the Springer correspondence describes how irreducible representations of a Weyl group can be realised in terms of a convolution action on
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)

High dimensional expanders – Alexander Lubotzky – ICM2018
Plenary Lecture 13 High dimensional expanders Alexander Lubotzky Abstract: Expander graphs have been, during the last five decades, the subject of a most fruitful interaction between pure mathematics and computer science, with influence and applications going both ways. In the last decad
From playlist Plenary Lectures

Geordie Williamson: Miraculous Treumann-Smith theory and geometric Satake
Abstract: This talk will be about geometric approaches to the representation theory of reductive algebraic groups in positive characteristic p. A cornerstone of the geometric theory is the geometric Satake equivalence, which gives an incarnation of the category of representations as a cate
From playlist Geordie Williamson: Representation theory and the Geometric Satake

On Finite Types That Are Not h-Sets - Sergey Melikhov
Sergey Melikhov Steklov Mathematical Institute; Member, School of Mathematics February 14, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics
