
Reconsidering natural numbers and arithmetical expressions | Data structures Math Foundations 185
It is time to turn our gaze back to the true foundations of the subject: arithmetic with natural numbers. But now we know that the issue of "What exactly is a natural number?" is fraught with subtlety. We adopt a famous dictum of Errett Bishop, and start to make meaningful distinctions bet
From playlist Math Foundations

Proof: What is it, and how does it work?
From playlist The Nature of Proof

Introduction to Direct Proofs: If n is even, then n squared is even
This video introduces the mathematical proof method of direct proof provides an example of a direct proof. mathispower4u.com
From playlist Symbolic Logic and Proofs (Discrete Math)

Proof by Induction: 4^n - 1 is a Multiple of 3
This video provides an example of proof by induction. mathispower4u.com
From playlist Sequences (Discrete Math)

Multisets and a new framework for arithmetic | Data Structures Math Foundations 187
Here we go back to the first videos in this series and recast that discussion in a more solid direction by utilizing our understanding of multisets. The crucial point is to define what a natural number is in a clear way. This issue is far more subtle than is generally acknowledged. For u
From playlist Math Foundations

Every Subset of a Linearly Independent Set is also Linearly Independent Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys A proof that every subset of a linearly independent set is also linearly independent.
From playlist Proofs

Using mathematical induction to prove a formula
👉 Learn how to apply induction to prove the sum formula for every term. Proof by induction is a mathematical proof technique. It is usually used to prove that a formula written in terms of n holds true for all natural numbers: 1, 2, 3, . . . To prove by induction, we first show that the f
From playlist Sequences
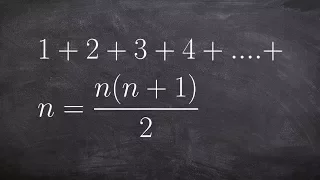
Learn how to use mathematical induction to prove a formula
👉 Learn how to apply induction to prove the sum formula for every term. Proof by induction is a mathematical proof technique. It is usually used to prove that a formula written in terms of n holds true for all natural numbers: 1, 2, 3, . . . To prove by induction, we first show that the f
From playlist Sequences

Well Ordering and Induction: Part 2
This was recorded as supplemental material for Math 115AH at UCLA in the spring quarter of 2020. In this video, I discuss the "philosophical importance" of induction, and go over two proofs that use the Principle of Mathematical Induction and the Well-Ordering Principle, respectively.
From playlist Well Ordering and Induction

Billy Price and Will Troiani present a series of seminars on foundations of mathematics. In this seminar Billy introduces natural deduction as a proof system. You can join this seminar from anywhere, on any device, at https://www.metauni.org. This video was filmed in Deprecation (https:/
From playlist Foundations seminar

Foundations - Seminar 6 - Discharging hypotheses and Curry-Howard
Daniel Murfet discusses the introduction and elimination rule for implication in natural deduction, the way in which undischarged hypotheses are managed, the "identity" of natural deductions (which deductions count as "the same") and how all of this feeds into the Curry-Howard (CH) corresp
From playlist Foundations seminar

Introduction to the Coq Proof Assistant - Andrew Appel
Introduction to the Coq Proof Assistant - Andrew Appel Princeton University December 7, 2010 A "proof assistant" is a software package comprising a validity checker for proofs in a particular logic, accompanied by semi-decision procedures called "tactics" that assist the mathematician in
From playlist Mathematics

How to Prove that a Sequence of Functions Converges Pointwise
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to Prove that a Sequence of Functions Converges Pointwise
From playlist Advanced Calculus

Ultraproducts: What are they good for?
From playlist Workshop on Model Theory, Differential/Difference Algebra, and Applications

IMS Public Lecture - Can Every Mathematical Problem Be Solved?
Menachem Magidor, The Hebrew University of Jerusalem, Israel
From playlist Public Lectures

1 + 2 + 3 + 4 + 5 + 6 + ... = –1/12 | Six proofs | Divergent Series
This video presents six proofs of the famous sum of the monotonic divergent series of natural numbers 1 + 2 + 3 + 4 + 5 + 6 + ... = –1/12 00:00 Introduction 00:15 Proof 1 – Generating Function 03:49 Proof 2 – Direct Calculation 06:50 Proof 3 – Intercept Function 11:13 Proof 4 – Partia
From playlist Summer of Math Exposition 2 videos

Fundamentals of Mathematics - Lecture 07: Methods of Proof
course page: http://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html handouts - DZB, Emory videography - Eric Melton
From playlist Fundamentals of Mathematics

Introduction to Proof by Induction: Prove 1+3+5+…+(2n-1)=n^2
This video introduces proof by induction and proves 1+3+5+…+(2n-1) equals n^2. mathispower4u.com
From playlist Sequences (Discrete Math)

Topology Without Tears - Video 4d - Writing Proofs in Mathematics
This is part (d) of the fourth video in a series of videos which supplement my online book "Topology Without Tears" which is available free of charge at www.topologywithouttears.net Video 4 focusses on the extremely important topic of writing proofs. This video is about Mathematical Induc
From playlist Topology Without Tears
