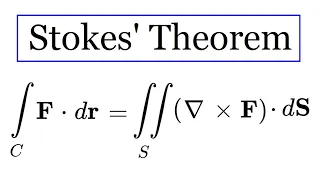Integration on manifolds | Duality theories | Differential forms | Theorems in calculus | Theorems in differential geometry | Differential topology
Generalized Stokes theorem
In vector calculus and differential geometry the generalized Stokes theorem (sometimes with apostrophe as Stokes' theorem or Stokes's theorem), also called the Stokes–Cartan theorem, is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. In particular, the fundamental theorem of calculus is the special case where the manifold is a line segment, and Stokes' theorem is the case of a surface in . Hence, the theorem is sometimes referred to as the Fundamental Theorem of Multivariate Calculus. Stokes' theorem says that the integral of a differential form over the boundary of some orientable manifold is equal to the integral of its exterior derivative over the whole of , i.e., Stokes' theorem was formulated in its modern form by Élie Cartan in 1945, following earlier work on the generalization of the theorems of vector calculus by Vito Volterra, Édouard Goursat, and Henri Poincaré. This modern form of Stokes' theorem is a vast generalization of a classical result that Lord Kelvin communicated to George Stokes in a letter dated July 2, 1850. Stokes set the theorem as a question on the 1854 Smith's Prize exam, which led to the result bearing his name. It was first published by Hermann Hankel in 1861. This classical case relates the surface integral of the curl of a vector field over a surface (that is, the flux of ) in Euclidean three-space to the line integral of the vector field over the surface boundary (also known as the loop integral). Classical generalizations of the fundamental theorem of calculus like the divergence theorem, and Green's theorem from vector calculus are special cases of the general formulation stated above after making a standard identification of vector fields with differential forms (different for each of the classical theorems). (Wikipedia).