
This is a second lecture on "Stochastic Yang-Mills" by Professor Martin Hairer. For more materials and slides visit: https://sites.google.com/view/oneworld-pderandom/home
From playlist Summer School on PDE & Randomness

Representation Theory as Gauge Theory - David Ben-Zvi [2016]
Slides for this talk: https://drive.google.com/file/d/1FHl_tIOjp26vuULi0gkSgoIN7PMnKLXK/view?usp=sharing Notes for this talk: https://drive.google.com/file/d/1BpP2Sz_zHWa_SQLM6DC6T8b4v_VKZs1A/view?usp=sharing David Ben-Zvi (University of Texas, Austin) Title: Representation Theory as G
From playlist Number Theory

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https://twitter.com/worldscienceu
From playlist Science Unplugged: General Relativity

In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than
From playlist Physics

Michael Wibmer: Etale difference algebraic groups
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Group Theory for Physicists (Definitions with Examples)
In this video, we cover the most basic points that a physicist should know about group theory. Along the way, we'll give you lots of examples that illustrate each step. 00:00 Introduction 00:11 Definition of a Group 00:59 (1) Closure 01:34 (2) Associativity 02:02 (3) Identity Element 03:
From playlist Mathematical Physics
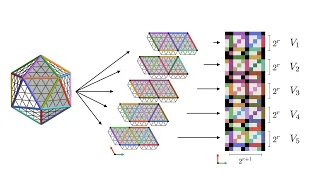
AMMI Course "Geometric Deep Learning" - Lecture 10 (Gauges) - Taco Cohen
Video recording of the course "Geometric Deep Learning" taught in the African Master in Machine Intelligence in July-August 2021 by Michael Bronstein (Imperial College/Twitter), Joan Bruna (NYU), Taco Cohen (Qualcomm), and Petar Veličković (DeepMind) Lecture 10: Gauges • Gauge transformat
From playlist AMMI Geometric Deep Learning Course - First Edition (2021)

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Yang-Mills for mathematicians (Lecture - 01) by Sourav Chatterjee
INFOSYS-ICTS RAMANUJAN LECTURES SOME OPEN QUESTIONS ABOUT SCALING LIMITS IN PROBABILITY THEORY SPEAKER Sourav Chatterjee (Stanford University, California, USA) DATE & TIME 14 January 2019 to 18 January 2019 VENUE Madhava Lecture Hall, ICTS campus GALLERY Lecture 1: Yang-Mills for mathemat
From playlist Infosys-ICTS Ramanujan Lectures

AMMI 2022 Course "Geometric Deep Learning" - Lecture 10 (Gauges) - Taco Cohen
Video recording of the course "Geometric Deep Learning" taught in the African Master in Machine Intelligence in July 2022 by Michael Bronstein (Oxford), Joan Bruna (NYU), Taco Cohen (Qualcomm), and Petar Veličković (DeepMind) Lecture 10: Gauges • Gauge transformations • Examples of gauge
From playlist AMMI Geometric Deep Learning Course - Second Edition (2022)

A Mathematical Introduction to 3d N = 4 Gauge Theories (Lecture 1) by Mathew Bullimore
PROGRAM : QUANTUM FIELDS, GEOMETRY AND REPRESENTATION THEORY 2021 (ONLINE) ORGANIZERS : Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pan
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Recent Results on Finite Group Lattice Gauge Theories - Sky Yang Cao
Members' Colloquium Topic: Recent Results on Finite Group Lattice Gauge Theories Speaker: Sky Yang Cao Affiliation: Member, School of Mathematics Date: March 20, 2023 The rigorous study of spin systems such as the Ising model is currently one of the most active research areas in probabil
From playlist Mathematics

Instantons and Monopoles (Lecture 1) by Sergey Cherkis
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Washington Taylor - How Natural is the Standard Model in the String Landscape?
Mike's pioneering work in taking a statistical approach to string vacua has contributed to an ever-improving picture of the landscape of solutions of string theory. In this talk, we explore how such statistical ideas may be relevant in understanding how natural different realizations of th
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Nikita Nekrasov - Non-perturbative Dyson-Schwinger equations...
Nikita NEKRASOV (Simons Center for Geometry and Physics, Stony Brook, USA)
From playlist Algèbre, Géométrie et Physique : une conférence en l'honneur

PiTP 2015 - "A Theory of Symmetry Protected Topological (3 of 3)" - Xiao-Gang Wen
https://pitp2015.ias.edu/
From playlist 2015 Prospects in Theoretical Physics Program

Gauge bosons, the glue that holds everything together: from fizzics.org
A gauge boson is a force carrier. An exchange particle that acts between fundamental particles conveying one of the four forces recognised in the standard model. This video is a brief introduction and description of these four, the photon conveying the electromagnetic force. The graviton (
From playlist Atomic structure
