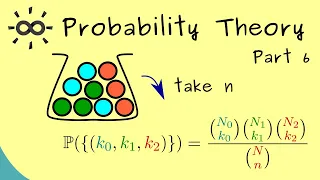
Fisher's noncentral hypergeometric distribution
In probability theory and statistics, Fisher's noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where sampling probabilities are modified by weight factors. It can also be defined as the conditional distribution of two or more binomially distributed variables dependent upon their fixed sum. The distribution may be illustrated by the following urn model. Assume, for example, that an urn contains m1 red balls and m2 white balls, totalling N = m1 + m2 balls. Each red ball has the weight ω1 and each white ball has the weight ω2. We will say that the odds ratio is ω = ω1 / ω2. Now we are taking balls randomly in such a way that the probability of taking a particular ball is proportional to its weight, but independent of what happens to the other balls. The number of balls taken of a particular color follows the binomial distribution. If the total number n of balls taken is known then the conditional distribution of the number of taken red balls for given n is Fisher's noncentral hypergeometric distribution. To generate this distribution experimentally, we have to repeat the experiment until it happens to give n balls. If we want to fix the value of n prior to the experiment then we have to take the balls one by one until we have n balls. The balls are therefore no longer independent. This gives a slightly different distribution known as Wallenius' noncentral hypergeometric distribution. It is far from obvious why these two distributions are different. See the entry for noncentral hypergeometric distributions for an explanation of the difference between these two distributions and a discussion of which distribution to use in various situations. The two distributions are both equal to the (central) hypergeometric distribution when the odds ratio is 1. Unfortunately, both distributions are known in the literature as "the" noncentral hypergeometric distribution. It is important to be specific about which distribution is meant when using this name. Fisher's noncentral hypergeometric distribution was first given the name extended hypergeometric distribution (Harkness, 1965), and some authors still use this name today. (Wikipedia).