Noncentral hypergeometric distributions
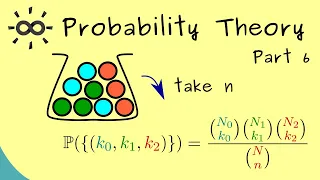
In statistics, the hypergeometric distribution is the discrete probability distribution generated by picking colored balls at random from an urn without replacement. Various generalizations to this distribution exist for cases where the picking of colored balls is biased so that balls of one color are more likely to be picked than balls of another color. This can be illustrated by the following example. Assume that an opinion poll is conducted by calling random telephone numbers. Unemployed people are more likely to be home and answer the phone than employed people are. Therefore, unemployed respondents are likely to be over-represented in the sample. The probability distribution of employed versus unemployed respondents in a sample of n respondents can be described as a noncentral hypergeometric distribution. The description of biased urn models is complicated by the fact that there is more than one noncentral hypergeometric distribution. Which distribution one gets depends on whether items (e.g., colored balls) are sampled one by one in a manner in which there is competition between the items or they are sampled independently of one another. The name noncentral hypergeometric distribution has been used for both of these cases. The use of the same name for two different distributions came about because they were studied by two different groups of scientists with hardly any contact with each other. Agner Fog (2007, 2008) suggested that the best way to avoid confusion is to use the name Wallenius' noncentral hypergeometric distribution for the distribution of a biased urn model in which a predetermined number of items are drawn one by one in a competitive manner and to use the name Fisher's noncentral hypergeometric distribution for one in which items are drawn independently of each other, so that the total number of items drawn is known only after the experiment. The names refer to Kenneth Ted Wallenius and R. A. Fisher, who were the first to describe the respective distributions. Fisher's noncentral hypergeometric distribution had previously been given the name extended hypergeometric distribution, but this name is rarely used in the scientific literature, except in handbooks that need to distinguish between the two distributions. (Wikipedia).