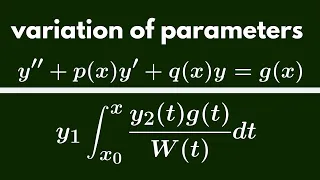Partial differential equations
In mathematics, Fisher's equation (named after statistician and biologist Ronald Fisher) also known as the Kolmogorov–Petrovsky–Piskunov equation (named after Andrey Kolmogorov, Ivan Petrovsky, and Nikolai Piskunov), KPP equation or Fisher–KPP equation is the partial differential equation: It is a kind of reaction–diffusion system that can be used to model population growth and wave propagation. (Wikipedia).
Differential Equations | Exact Equations and Integrating Factors Example 2
We give an example of converting a non-exact differential equation into an exact equation. We use this to solve the differential equation.
From playlist Numerical Methods for Differential Equations
Differential Equations | Variation of Parameters.
We derive the general form for a solution to a differential equation using variation of parameters. http://www.michael-penn.net
From playlist Differential Equations
The Definition of a Linear Equation in Two Variables
This video defines a linear equation in to variables and provides examples of the different forms of linear equations. http://mathispower4u.com
From playlist The Coordinate Plane, Plotting Points, and Solutions to Linear Equations in Two Variables
Differential Equations | Variation of Parameters Example 2
We solve a second order linear differential equation using the method of variation of parameters.
From playlist Differential Equations
Differential Equations | Homogeneous System of Differential Equations Example 1
We solve a homogeneous system of first order linear differential equations with constant coefficients using the matrix exponential. This example involves a matrix which is diagonalizable with real eigenvalues. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations
B25 Example problem solving for a Bernoulli equation
See how to solve a Bernoulli equation.
From playlist Differential Equations
Differential Equations | Variation of Parameters Example 1
We solve a second order linear differential equation using the method of variation of parameters.
From playlist Differential Equations
The Derivative of a Constant Example with y = 2
The Derivative of a Constant Example with y = 2
From playlist Random calculus problems:)
12. Overlapping Generations Models of the Economy
Financial Theory (ECON 251) In order for Social Security to work, people have to believe there's some possibility that the world will last forever, so that each old generation will have a young generation to support it. The overlapping generations model, invented by Allais and Samuelso
From playlist Financial Theory with John Geanakoplos
Sloppiness and Parameter Identifiability, Information Geometry by Mark Transtrum
26 December 2016 to 07 January 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore Information theory and computational complexity have emerged as central concepts in the study of biological and physical systems, in both the classical and quantum realm. The low-energy landscape of classical
From playlist US-India Advanced Studies Institute: Classical and Quantum Information
Differential Equations | Homogeneous System of Differential Equations Example 2
We solve a homogeneous system of linear differential equations with constant coefficients using the matrix exponential. In this case the associated matrix is 2x2 and not diagonalizable. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations
5. Present Value Prices and the Real Rate of Interest
Financial Theory (ECON 251) Philosophers and theologians have railed against interest for thousands of years. But that is because they didn't understand what causes interest. Irving Fisher built a model of financial equilibrium on top of general equilibrium (GE) by introducing time and
From playlist Financial Theory with John Geanakoplos
Restoring Heisenberg scaling in noisy quantum metrology (...) - M. Genoni - Workshop 2 - CEB T2 2018
Marco Genoni (Univ. Milano) / 06.06.2018 Restoring Heisenberg scaling in noisy quantum metrology by monitoring the environment We study quantum frequency estimation for N qubits subjected to independent Markovian noise, via strategies based on time-continuous monitoring of the environmen
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments
Oxford Mathematics Public Lectures: Alison Etheridge - Modelling Genes How can we explain the patterns of genetic variation in the world around us? The genetic composition of a population can be changed by natural selection, mutation, mating, and other genetic, ecological and evolutionary
From playlist Oxford Mathematics Public Lectures
The Grand Unified Theory of Quantum Metrology - R. Demkowicz-Dobrzanski - Workshop 1 - CEB T2 2018
Rafal Demkowicz-Dobrzanski (Univ. Warsaw) / 15.05.2018 The Grand Unified Theory of Quantum Metrology A general model of unitary parameter estimation in presence of Markovian noise is considered, where the parameter to be estimated is associated with the Hamiltonian part of the dynamics.
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments
6. Irving Fisher's Impatience Theory of Interest
Financial Theory (ECON 251) Building on the general equilibrium setup solved in the last week, this lecture looks in depth at the relationships between productivity, patience, prices, allocations, and nominal and real interest rates. The solutions to three of Fisher's famous examples ar
From playlist Financial Theory with John Geanakoplos
6. Maximum Likelihood Estimation (cont.) and the Method of Moments
MIT 18.650 Statistics for Applications, Fall 2016 View the complete course: http://ocw.mit.edu/18-650F16 Instructor: Philippe Rigollet In this lecture, Prof. Rigollet continued on maximum likelihood estimators and talked about Weierstrass Approximation Theorem (WAT), and statistical appli
From playlist MIT 18.650 Statistics for Applications, Fall 2016
4. Efficiency, Assets, and Time
Financial Theory (ECON 251) Over time, economists' justifications for why free markets are a good thing have changed. In the first few classes, we saw how under some conditions, the competitive allocation maximizes the sum of agents' utilities. When it was found that this property didn'
From playlist Financial Theory with John Geanakoplos
13. Demography and Asset Pricing: Will the Stock Market Decline when the Baby Boomers Retire?
Financial Theory (ECON 251) In this lecture, we use the overlapping generations model from the previous class to see, mathematically, how demographic changes can influence interest rates and asset prices. We evaluate Tobin's statement that a perpetually growing population could solve t
From playlist Financial Theory with John Geanakoplos
Illustrates the solution of a Bernoulli first-order differential equation. Free books: http://bookboon.com/en/differential-equations-with-youtube-examples-ebook http://www.math.ust.hk/~machas/differential-equations.pdf
From playlist Differential Equations with YouTube Examples