
Theory of numbers: Fermat's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Fermat's theorem a^p = a mod p. We then define the order of a number mod p and use Fermat's theorem to show the order of a divides p-1. We apply this to testing some Fermat and Mersenne numbers to se
From playlist Theory of numbers

In this video we introduce Fermat's little theorem and give a proof using congruences. The content of this video corresponds to Section 7.2 of my book "Number Theory and Geometry" which you can find here: https://alozano.clas.uconn.edu/number-theory-and-geometry/
From playlist Number Theory and Geometry

From playlist L. Number Theory

Number Theory | A very special case of Fermat's Last Theorem
We prove a very simple case of Fermat's Last Theorem. Interestingly, this case is fairly easy to prove which highlights the allure of the theorem as a whole -- especially given the fact that much of modern number theory was developed as part of the program that ended in the full proof. ht
From playlist Number Theory
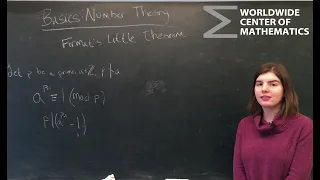
Number Theory: Fermat's Little Theorem
An introduction to Fermat's Little Theorem and its applications
From playlist Basics: Number Theory

Fermat's Little Theorem ← Number Theory
Fermat's Little Theorem was observed by Fermat and proven by Euler, who generalized the theorem significantly. This theorem aids in dividing extremely large numbers and can aid in testing numbers to see if they are prime. For more advanced students, this theorem can be easily proven usin
From playlist Number Theory
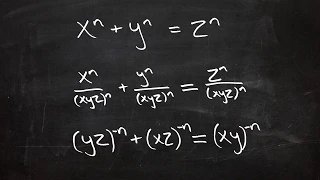
Fermat's Last Theorem for rational and irrational exponents
Fermat's Last Theorem states the equation x^n + y^n = z^n has no integer solutions for positive integer exponents greater than 2. However, Fermat's Last Theorem says nothing about exponents that are not positive integers. Note: x, y and z are meant to be positive integers, which I should
From playlist My Maths Videos

Number Theory | Fermat's Little Theorem
We state and prove Fermat's Little Theorem. www.michael-penn.net
From playlist Number Theory

Theory of numbers: Congruences: Euler's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Euler's theorem, a generalization of Fermat's theorem to non-prime moduli, by using Lagrange's theorem and group theory. As an application of Fermat's theorem we show there are infinitely many prim
From playlist Theory of numbers

Introduction to number theory lecture 1.
This lecture is the first lecture of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 This lecture gives a survey of some of the topics covered later in the course,
From playlist Introduction to number theory (Berkeley Math 115)

What's the Geometry of Numbers? - Minkowski's Theorem #SoME2
We're looking at Minkowski's Geometry of Numbers Theorem and applying it to prove the so-called Fermat's Christmas Theorem. #SoME2 Timetable: 0:00 - Introduction 1:55 - Symmetric Convex Bodies 3:28 - Proving the Main Theorem 7:00 - Other Lattices 7:44 - Fermat's Christmas Theorem 10:35 -
From playlist Summer of Math Exposition 2 videos

Polygonal Numbers - Geometric Approach & Fermat's Polygonal Number Theorem
I created this video with the YouTube Video Editor (http://www.youtube.com/editor)
From playlist ℕumber Theory

Theory of numbers:Introduction
This lecture is part of an online undergraduate course on the theory of numbers. This is the introductory lecture, which gives an informal survey of some of the topics to be covered in the course, such as Diophantine equations, quadratic reciprocity, and binary quadratic forms.
From playlist Theory of numbers

Visual Group Theory, Lecture 6.8: Impossibility proofs
Visual Group Theory, Lecture 6.8: Impossibility proofs The ancient Greeks sought basic ruler and compass constructions such as (1) squaring the circle, (2) doubling the cube, and (3) trisecting an angle. In the previous lecture, we learned how a length or angle 'z' is constructable iff th
From playlist Visual Group Theory

Q&A - Topology, geometry and life in three dimensions
Caroline Series answers questions following her Friday Evening Discourse. What would the solar system look like in a universe with hyperbolic geometry? Was the proof of Fermat’s last theorem or the Poincare conjecture more exciting? Subscribe for regular science videos: http://bit.ly/RiSu
From playlist Ri Talks

Video recording of the mega favourite number of a good friend. Fermat Primes on the OEIS: https://oeis.org/A019434 Video created using a colourful combination of DaVinci Resolve, Audacity, GIMP and TeXstudio. Music: Wholesome by Kevin MacLeod Link: https://incompetech.filmmusic.io/
From playlist MegaFavNumbers

Heptadecagon and Fermat Primes (the math bit) - Numberphile
Main (previous) video: http://youtu.be/87uo2TPrsl8 David Eisenbud from MSRI on the math behind the 17-gon and other constructible polygons. NUMBERPHILE Website: http://www.numberphile.com/ Numberphile on Facebook: http://www.facebook.com/numberphile Numberphile tweets: https://twitter.com
From playlist David Eisenbud on Numberphile

Episode 7: Integration - The Mechanical Universe
Episode 7. Integration: Newton and Leibniz arrive at the conclusion that differentiation and integration are inverse processes. “The Mechanical Universe,” is a critically-acclaimed series of 52 thirty-minute videos covering the basic topics of an introductory university physics course. E
From playlist The Mechanical Universe

Proof based on a comment of an earlier video - an example of Fermat Little Theorem
#mathonshorts #shorts Credit goes to "black third" https://www.youtube.com/channel/UCWt0aCW6TeP8PP5pdREfoag See comments from this video: https://youtu.be/NKpzfyCZAPg The Pigeonhole Principle was used in the other video. Here, we use Fermat Little Theorem to prove that the number of
From playlist Elementary Number Theory

Theory of numbers: Quadratic reciprocity
This lecture is part of an online undergraduate course on the theory of numbers. We state and law of quadratic reciprocity for Legendre symbols, and prove it using Gauss sums. As applications we show how to use it to calculate Legendre symbols and to test Fermat numbers to see if they are
From playlist Theory of numbers