
Saturn: Best Rings in the Solar System
I think that nine out of ten people, if you ask them to picture a planet in their minds, will picture Saturn. Why? It's those rings! They are irresistible. Rings are to planets as peanut butter is to chocolate. The perfect complement. But there is much more to Saturn than just its rings. T
From playlist Astronomy/Astrophysics

An excellent song which I could not find on Youtube.
From playlist the absolute best of stereolab

Follow Christian Löffler: http://www.christian-loeffler.net https://web.facebook.com/christianloefflerofficial https://soundcloud.com/christianloeffler Tracklist: 1. Myiami 2. Athlete 3. Neo 4. Mosaics 5. lid 6. Silk 7. Haul 8. Wilderness 9. Swim
From playlist Classical

Feeding Excelopolis from the FMWC Open on ESPN3 - 2447
December 4th 2021 is a red-letter day for Microsoft Excel. It is the first day that an Excel competition was carried live on the ESPN family of networks. Watch again on Wednesday December 8: https://www.espn.com/watch/schedule/_/type/upcoming/categoryId/634d383d-6f26-39cd-9efa-feb4eff2354
From playlist Excel Functions

CTNT 2022 - Algebraic Number Theory (Lecture 2) - by Hanson Smith
This video is part of a mini-course on "Algebraic Number Theory" that was taught during CTNT 2022, the Connecticut Summer School and Conference in Number Theory. More about CTNT: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2022 - Algebraic Number Theory (by Hanson Smith)

Excel Magic Trick 972: Empty Cell or Null Text String in Formulas: Counting Formulas
Download Excel Start File: https://people.highline.edu/mgirvin/YouTubeExcelIsFun/EMT971-975.xlsx Download Excel File: http://people.highline.edu/mgirvin/ExcelIsFun.htm Learn about the different between Empty Cell and Null Text String. Counting formulas 1. Empty (Null Text String is NOT co
From playlist Excel Series: Magic Tricks (5th 200 videos)

Speak Softly Love Classic version. "The Godfather" theme song. (please comment and rate :D)
From playlist Brilliant Music

CTNT 2022 - Algebraic Number Theory (Lecture 3) - by Hanson Smith
This video is part of a mini-course on "Algebraic Number Theory" that was taught during CTNT 2022, the Connecticut Summer School and Conference in Number Theory. More about CTNT: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2022 - Algebraic Number Theory (by Hanson Smith)

Commutative algebra 1 (Introduction)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. https://link.springer.com/book/10.1007/978-1-4612-5350-1 This is a short introductory lecture, and gives a few examples of the
From playlist Commutative algebra

Moritz Kerz: Algebraic K-theory and descent for blow-ups (Lecture 2)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Moritz Kerz: Algebraic K-theory and descent for blow-ups Abstract: It is well-known that special cases of descent along blow-ups for algebraic K-theory play an important role for ca
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Excel Secret Decoder Ring - 2330
This started as an April Fools joke from Bill Szysz and Mike Girvin, but it brought back memories of Schoolhouse Rock from 1973 and the story of Little Twelve Toes. In today's video, a secret decoder ring in Excel using BASE and DECIMAL. Also: you can now assign fill color and font colors
From playlist New in 2020
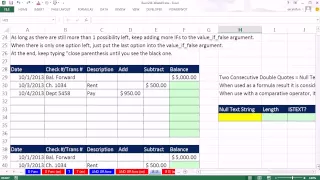
Highline Excel 2013 Class Video 15: IF & IS Functions To Deliver Numbers, Text, Formulas, Nested IFs
Download workbook: http://people.highline.edu/mgirvin/AllClasses/214_2013/214/Busn214_2013.htm This is the Highline Community College Class, Spreadsheet Construction taught by Michael Girvin: Basic To Advanced Excel. Topics in this video: 1. IF Function to deliver numbers (00:33 min) 2. IF
From playlist Excel Formulas - Basics and Beyond

Moritz Kerz - On the vanishing of negative K-theory
Weibel's conjecture predicts that negative algebraic K-theory vanishes in degrees less than minus the dimension of the ring. The conjecture is known in characteristic zero. In the talk I will explain an approach which reduces the general conjecture to a very weak form of resolution of sin
From playlist Séminaire Grothendieck 30 mars 2016

Synthesis Workshop: Total Synthesis of Ambruticin J with James Bowen (Episode 62)
In this Research Spotlight episode, we are joined by James Bowen (Willis group, University of Bristol), who takes us through his work on the total synthesis of ambruticin J. Key reference: Org. Biomol. Chem. 2021, 19, 6210–6215. Other references (in order of appearance): Höfle, G. et al
From playlist Research Spotlights





