
Algebra Ch 46: Exponential Functions (9 of 12) How to Calculate Euler's Number? Method 2
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn how to calculate Euler's number using infinite series, e=2.718281828459... (Method 2) Next video in this series can b
From playlist THE "HOW TO" PLAYLIST

Algebra Ch 46: Exponential Functions (8 of 12) How to Calculate Euler's Number? Method 1
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn how to calculate Euler's number, e=2.718281828459... (Method 1) Next video in this series can be seen at: https://you
From playlist THE "HOW TO" PLAYLIST

Algebra Ch 46: Exponential Functions (7 of 12) What is Euler's Number?
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn Eulers's number is also known as the “natural number” and the exponential function becomes f(x)=e^x or f(x)=e^(cx) wher
From playlist THE "WHAT IS" PLAYLIST

This video given Euler's identity, reviews how to derive Euler's formula using known power series, and then verifies Euler's identity with Euler's formula http://mathispower4u.com
From playlist Mathematics General Interest

All the Ways of Defining e | Is Euler's Number Geometric? -- Part 1
Part 2: https://youtu.be/YgScek3GkdI The full series on Euler's number: Part 1: https://youtu.be/rbmUqseGOOM Part 2: https://youtu.be/YgScek3GkdI Part 3: https://youtu.be/c7ilUAqAxyU Part 4: https://youtu.be/oU5elvZL0uU Part 5: https://youtu.be/EoFhgYySUgk Given any conversation between
From playlist Is Euler's Number Geometric?

Euler's number, derivatives, and the bank at the end of the universe
Euler's number, e, is defined as a limit. The function e to the x is (up to multiplying by a constant) the only function that is its own derivative. How are these two related? In this video you'll find an explanation for this phenomenon using banking interest rates, and a very particular b
From playlist Mathematics videos

Euler's formulas, Rodrigues' formula
In this video I proof various generalizations of Euler's formula, including Rodrigues' formula and explain their 3 dimensional readings. Here's the text used in this video: https://gist.github.com/Nikolaj-K/eaaa80861d902a0bbdd7827036c48af5
From playlist Algebra

Euler Pronunciation: In Depth Analysis
Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, but it will help to support my channel. Thank you! ►PRODUCT RECOMMENDATIONS https://www.amazon.com/shop/brithema
From playlist Fun and Amazing Math

Mandelbrot fractal zoom // featuring Euler bio
Mandelbrot fractal zoom // featuring Euler bio Come hang out and watch a fractal zoom through the Mandelbrot set. To celebrate Euler's contributions to mathematics, this video features a brief bio. of Leonhard Euler! ---------------------------------------------------------------------
From playlist Misc.

What are geometric numbers? | Is Euler's Number Geometric? -- Part 3
Part 4: https://youtu.be/oU5elvZL0uU The full series on Euler's number: Part 1: https://youtu.be/rbmUqseGOOM Part 2: https://youtu.be/YgScek3GkdI Part 3: https://youtu.be/c7ilUAqAxyU Part 4: https://youtu.be/oU5elvZL0uU Part 5: https://youtu.be/EoFhgYySUgk Given any conversation between
From playlist Is Euler's Number Geometric?

Math Explorations Ep22, Euler circuits & paths (Mar 23, 2022)
This is a recording of a live class for Math 1015, Mathematics: An Exploration, an undergraduate course for non-technical majors at Fairfield University, Spring 2022. The major topics are voting, gerrymandering, and graph theory. Handouts and homework are at the class website. Class web
From playlist Math 1015 (Mathematical Explorations) Spring 2022

MA 15: Euler circuits and paths
This video is for my Spring 2020 section of MA 15, for the class meeting on Friday April 3. Fast forward music is from "Now Get Busy" by the Beastie Boys, licensed Creative Commons Noncommercial Sampling Plus.
From playlist Math 15 Spring 2020

Math for Liberal Studies - Lecture 1.2.1 Euler's Theorem
This is the first video lecture for Math for Liberal Studies Section 1.2: Finding Euler Circuits. In this lecture, we learn about Euler's Theorem, which tells us how to detect whether a given graph has an Euler circuit or not. I also explain why Euler's Theorem works the way it does.
From playlist Math for Liberal Studies Lectures
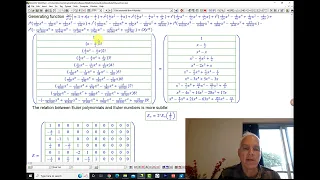
Advice for amateur mathematicians | More magic, with Euler numbers and Euler polynomials | Wild Egg
From the Bernoulli numbers and Bernoulli polynomials, it is a small step to consider Euler numbers and Euler polynomials. We of course pursue our basic strategy of incorporating these things into our two dimensional number theoretic point of view, and then utilizing linear algebra / matrix
From playlist Maxel inverses and orthogonal polynomials (non-Members)

Graph Theory: 24. Euler Trail iff 0 or 2 Vertices of Odd Degree
I begin by reviewing the proof that a graph has an Euler tour if and only if every vertex has even degree. Then I show a proof that a graph has an Euler trail if and only it has either 0 or 2 vertices of odd degree. An introduction to Graph Theory by Dr. Sarada Herke. Related Videos: htt
From playlist Graph Theory part-5

[Discrete Mathematics] Euler Circuits and Euler Trails
We talk about euler circuits, euler trails, and do a proof. Visit our website: http://bit.ly/1zBPlvm Subscribe on YouTube: http://bit.ly/1vWiRxW *--Playlists--* Discrete Mathematics 1: https://www.youtube.com/playlist?list=PLDDGPdw7e6Ag1EIznZ-m-qXu4XX3A0cIz Discrete Mathematics 2: https:
From playlist Discrete Math 2
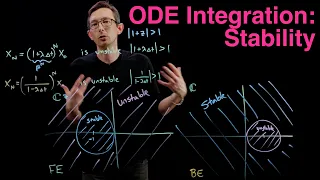
Stability of Forward Euler and Backward Euler Integration Schemes for Differential Equations
In this video, we explore the stability of the Forward Euler and Backward/Implicit Euler integration schemes. In particular, we investigate the eigenvalues of these discrete-time update equations, relating the eigenvalues to the stability of the algorithm. This basic stability analysis t
From playlist Engineering Math: Differential Equations and Dynamical Systems

This is a video that explains Euler Groups and incudes a coding demonstration for constructing the Cayley Table. The link to the JS Fiddle is: https://jsfiddle.net/colebabiuch/jpem1d73/10/
From playlist Summer of Math Exposition Youtube Videos

Michael BORINSKY - The Euler Characteristic of Out(Fn) and the Hopf Algebra of Graphs
In their 1986 work, Harer and Zagier gave an expression for the Euler characteristic of the moduli space of curves, M_gn, or equivalently the mapping class group of a surface. Recently, in joint work with Karen Vogtmann, we performed a similar analysis for Out(Fn), the outer automorphism g
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday