
Ex: Negative Fractions Raised to Powers
This video provides examples of raising negative fractions to powers. Complete Video Library at http://www.mathispower4u.com
From playlist Multiplying and Dividing Fractions

How to simplify a fraction raised to a negative exponent
👉 Learn how to simplify expressions using the power rule and the negative exponent rule of exponents. When several terms of an expression is raised to an exponent outside the parenthesis, the exponent is distributed over the individual terms in the expression and the exponent outside the p
From playlist Simplify Using the Rules of Exponents

Stirling numbers and Pascal triangles | Wild Linear Algebra A 23 | NJ Wildberger
When we interpret polynomials as sequences rather than as functions, new bases become important. The falling and rising powers play an important role in analysing general sequences through forward and backward difference operators. The change from rising powers to ordinary powers, and fro
From playlist WildLinAlg: A geometric course in Linear Algebra

Factorising Quadratics | Algebra | Maths | FuseSchool
Factorising Quadratics | Algebra | Maths | FuseSchool In this video we’re going to discover how to factorise quadratics. Quadratics are expressions with x2 as the highest power. Expanding and factorising are opposites. Factorising means to put into brackets, and with quadratics it is usua
From playlist MATHS

Ex: Factor Trinomials When A is NOT Equal to 1 - Grouping Method
This video provides examples of how to factor a trinomial when the leading coefficient is not equal to 1 by using the grouping method. Complete Video Listing: http://www.mathispower4u.com Search by Topic: http://www.mathispower4u.wordpress.com
From playlist Factoring Trinomials with a Leading Coefficient Not 1

Factoring Trinomials Leading Coefficient Not 1 by Grouping
Learn how to factor trinomials with leading coefficients by splitting the middle term and factoring by grouping in this free math video tutorial by Mario's Math Tutoring. 0:39 Example 1 Factor 2x^2 + 5x +2 by Splitting Middle Term and Factor by Grouping 2:37 Example 2 Factor 3x^2 - 26x +
From playlist Factoring - All Different Types

The Binomial Chu Vandermonde Identity: a new unification? | Algebraic Calculus Two | Wild Egg Maths
We suggest a novel unification of the Binomial and Chu Vandermonde identities, leading to an unusual introduction of the exponential polyseries, along with Newton's reciprocal polyseries. The main idea is to introduce a generalization of Knuth's rising and falling powers notation, which w
From playlist Algebraic Calculus Two

The Chu Vandermonde Identity | Algebraic Calculus Two | Wild Egg Maths
We introduce the Chu Vandermonde identity as a key ingredient in establishing Newton's polyseries theorem, which gives the fundamental multiplicative relation between the various extensions of the Binomial theorem that Newton discovered for rational powers. Along the way we look at the as
From playlist Algebraic Calculus Two

The Rise and Fall of Camden, New Jersey - America's most dangerous city - IT'S HISTORY
Get an amazing gift for your mom this Mother’s Day! Go to https://establishedtitles.com/Itshistory and get 10% off today. Thanks to Established Titles for sponsoring today's video. Camden City long served as the heart of the South Jersey region. Located directly across the Delaware River
From playlist New Jersey History

Ex: Factor Trinomials When A is NOT Equal to 1 - Bottoms Up Method
This video provides examples of how to factor a trinomial when the leading coefficient is not equal to 1 by using the bottoms up method. Complete Video Listing: http://www.mathispower4u.com Search by Topic: http://www.mathispower4u.wordpress.com
From playlist Factoring Trinomials with a Leading Coefficient Not 1

Factorise quadratic expressions 1
Powered by https://www.numerise.com/ Factorise quadratic expressions 1
From playlist Quadratics

Detroit's Tragic Downfall | The Rise and Fall of Detroit Michigan
Once one of America’s largest cities, Detroit was famously both a behemoth in automobile production and the birthplace of Motown. In recent years, however, it has been amid a financial and social decline—but it was not always this way. Today we will discover the rise and fall of Detroit.
From playlist Detroit History

Laws of Exponents Worked Example 12
In this video, we try a basic law of exponents problem. More exponent videos here: https://www.youtube.com/playlist?list=PLntYGYK-wJE2gom-s1y8UzeKVfn6tj-BZ
From playlist Laws of Exponents

027 Hydrogen part 3 Eigenfunctions
In this series of physics lectures, Professor J.J. Binney explains how probabilities are obtained from quantum amplitudes, why they give rise to quantum interference, the concept of a complete set of amplitudes and how this defines a "quantum state". Notes and problem sets here http://www
From playlist James Binney - 2nd Year Quantum Mechanics

Why Gary Indiana will Become a Ghost Town (The Rise and Fall of Gary Indiana) - IT'S HISTORY
Once the Magic City of America’s Rust Belt, Gary, Indiana is a city of a much different reputation today. From the greatest producer of American Steel and a key arm in the Arsenal of Democracy, it devolved into a murder capital until it ran out of people to kill. Its story is familiar, tho
From playlist Tales of Urban Decay

Mod-01 Lec-24 The economics of Marx
History of Economic Theory by Dr. Shivakumar, Department of Humanities and Social Sciences IIT Madras, For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist IIT Madras: History of Economic Theory | CosmoLearning.org Economics

Using end behavior, zeros and the intermediate value theorem to graph a polynomial
👉 Learn how to use the tools needed to graph a Polynomial function in standard form. The tools we will use to help us graph are end behavior, finding the zeros by factoring synthetic division as well as identify the multiplicity of each zero. The end behavior of the polynomial can be dete
From playlist Graph a Polynomial Function in Standard Form

Mod-01 Lec-19 Ricardo-Malthus debate
History of Economic Theory by Dr. Shivakumar, Department of Humanities and Social Sciences IIT Madras, For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist IIT Madras: History of Economic Theory | CosmoLearning.org Economics

Recent progress on Serre weight conjectures - Bao Le Hung
Topic: Recent progress on Serre weight conjectures Speaker: Bao Le Hung, University of Chicago Time/Room: 4:30pm - 5:30pm/S-101 More videos on http://video.ias.edu
From playlist Mathematics
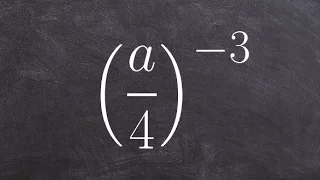
how to simplify an expression raised to a negative power
👉 Learn how to simplify expressions using the power rule and the negative exponent rule of exponents. When several terms of an expression is raised to an exponent outside the parenthesis, the exponent is distributed over the individual terms in the expression and the exponent outside the p
From playlist Simplify Using the Rules of Exponents