
Molecular and Empirical Formulas
Introduction to molecular and empirical formulas. Calculating molecular mass. More free lessons at: http://www.khanacademy.org/video?v=gfBcM3uvWfs
From playlist Chemistry

Empirical Formula | Chemistry | Homework Help
The Empirical formula is the lowest whole number ratio of the atoms of the elements in a compound. In this video, we show you how to calculate the empirical formula given the percent composition of a compound. We also talk about how the empirical formula and molecular formula are related.
From playlist Chemistry Lessons
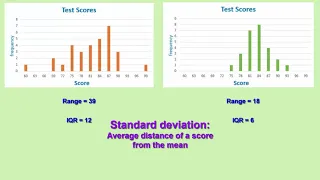
Introduction to standard deviation, IQR [Inter-Quartile Range], and range
From playlist Unit 1: Descriptive Statistics

Empirical vs Molecular Formula for Chemical Compounds
Explains the difference between the empirical formula and the molecular formula for chemical compounds. You can see a listing of all my videos at my website, http://www.stepbystepscience.com
From playlist Chemical Equations; Ionic and Covalent Compounds

Statistics: Ch 4 Probability in Statistics (20 of 74) Definition of Probability
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn the “strict” definition of experimental (empirical) and theoretical probability. Next video in this series can be seen
From playlist STATISTICS CH 4 STATISTICS IN PROBABILITY

Percentiles, Deciles, Quartiles
Understanding percentiles, quartiles, and deciles through definitions and examples
From playlist Unit 1: Descriptive Statistics

More Standard Deviation and Variance
Further explanations and examples of standard deviation and variance
From playlist Unit 1: Descriptive Statistics
The dispersion of data by means of the standard deviation.
From playlist Medical Statistics

Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set
https://www.patreon.com/ProfessorLeonard Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set
From playlist Statistics (Full Length Videos)

Empirical Measures along FPP Geodesics by Erik Bates
PROGRAM FIRST-PASSAGE PERCOLATION AND RELATED MODELS (HYBRID) ORGANIZERS Riddhipratim Basu (ICTS-TIFR, India), Jack Hanson (City University of New York, US) and Arjun Krishnan (University of Rochester, US) DATE & TIME 11 July 2022 to 29 July 2022 VENUE Ramanujan Lecture Hall and online Th
From playlist First-Passage Percolation and Related Models 2022 Edited

From playlist Contributed talks One World Symposium 2020

On a local Lyapunov function for the McKean-Vlasov dynamics by Rajesh Sundaresan
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Marios G. Stamatakis: Hydrodynamic limits and condensing zero range processes
Marios G. Stamatakis: Hydrodynamic limits and condensing zero range processes Condensing zero range processes are interacting particle systems with zero range interaction exhibiting phase separation at densities above a finite critical density. We prove the hydrodynamic limit of mean zer
From playlist HIM Lectures 2015

The circular law for sparse non-Hermitian random matrices by Anirban Basak
Speaker : Anirban Basak, Weizmann Institute of Science, Israel Date : Tuesday, October 10, 2017 Time : 4:00 PM Venue : Madhava Lecture Hall, ICTS Campus, Bangalore Abstract : Sparse matrices are abundant in statistics, neural network, financial modeling, electrica
From playlist ICTS Colloquia

Stanford EE104: Introduction to Machine Learning | 2020 | Lecture 6 - empirical risk minimization
Professor Sanjay Lall Electrical Engineering To follow along with the course schedule and syllabus, visit: http://ee104.stanford.edu To view all online courses and programs offered by Stanford, visit: https://online.stanford.edu/ 0:00 Introduction 0:26 Parametrized predictors 3:09 Tra
From playlist Stanford EE104: Introduction to Machine Learning Full Course
Colloquium MathAlp 2019 - Alice Guionnet
Entropies et grandes déviations pour les grandes matrices aléatoires Estimer la probabilité d'événements rares est un problème classique des probabilités depuis que Boltzmann a défini son entropie et que la mécanique statistique s'est développée. La théorie des grandes déviations donne
From playlist Colloquiums MathAlp

Jeannette Woerner: Limit theorems for Bessel and Dunkl processes of large dimensions
HYBRID EVENT Recorded during the meeting "Modern Analysis Related to Root Systems with Applications" the October 19, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathe
From playlist Virtual Conference

Statistics - How to use the Empirical Rule
In this video we cover how to use the Empirical Rule for normal (bell-shaped) distributions. Remember that for real-world data that only approximately follows a normal distribution, these values will give you approximate percentages. ▬▬ Chapters ▬▬▬▬▬▬▬▬▬▬▬ 0:00 Start 0:13 What is the
From playlist Statistics

Joscha Prochno: The large deviations approach to high-dimensional convex bodies, lecture III
Given any isotropic convex body in high dimension, it is known that its typical random projections will be approximately standard Gaussian. The universality in this central limit perspective restricts the information that can be retrieved from the lower-dimensional projections. In contrast
From playlist Workshop: High dimensional spatial random systems
