
In this talk, we will define elliptic curves and, more importantly, we will try to motivate why they are central to modern number theory. Elliptic curves are ubiquitous not only in number theory, but also in algebraic geometry, complex analysis, cryptography, physics, and beyond. They were
From playlist An Introduction to the Arithmetic of Elliptic Curves

Are they irrational? Transcendental? | Epic Math Time
Showing that a number is transcendental can be difficult. While π and e have a deep connection involving exponentiation, other combinations of them, like π + e, are not as well understood. Follow me on Instagram for previews, behind-the-scenes, and more content!: http://instagram.com/epic
From playlist Latest Uploads

Trigonometry in elliptic geometry | Universal Hyperbolic Geometry 41 | NJ Wildberger
We here introduce new laws for spherical and elliptic trigonometry. These are natural consequences of applying Rational Trigonometry to the three dimensional projective setting. Remarkably, the main laws end up being exactly the same as those in Universal Hyperbolic Geometry! It means ther
From playlist Universal Hyperbolic Geometry

Fermat’s HUGE little theorem, pseudoprimes and Futurama
A LOT of people have heard about Andrew Wiles solving Fermat's last theorem after people trying in vain for over 350 years. Today's video is about Fermat's LITTLE theorem which is at least as pretty as its much more famous bigger brother, which has a super pretty accessible proof and which
From playlist Recent videos

Application of Elliptic Curves to Cryptography
Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security
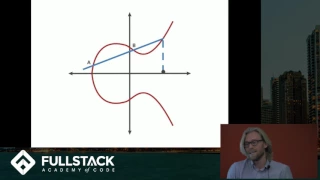
Elliptic Curve Cryptography Tutorial - Understanding ECC through the Diffie-Hellman Key Exchange
Learn more advanced front-end and full-stack development at: https://www.fullstackacademy.com Elliptic Curve Cryptography (ECC) is a type of public key cryptography that relies on the math of both elliptic curves as well as number theory. This technique can be used to create smaller, fast
From playlist Elliptic Curves - Number Theory and Applications
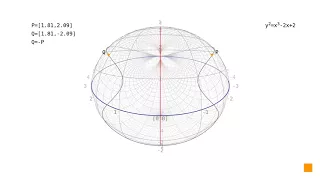
Elliptic curves: point at infinity in the projective plane
This video depicts point addition and doubling on elliptic curve in simple Weierstrass form in the projective plane depicted using stereographic projection where the point at infinity can actually be seen. Explanation is in the accompanying article https://trustica.cz/2018/04/05/elliptic-
From playlist Elliptic Curves - Number Theory and Applications

Spherical and elliptic geometries: an introduction | Universal Hyperbolic Geometry 33
We introduce PART II of this course on universal hyperbolic geometry: Bringin geometries together. This lecture introduces the very basic definitions of spherical geometry; lines as great circles, antipodal points, spherical triangles, circles, and some related notions on points, lines and
From playlist Universal Hyperbolic Geometry

"Fortunately, Unfortunately": How to Tell Whether a Number Is Prime #MegaFavNumbers
How can we tell whether or not a large integer is prime? Well, there's some bad news and some good news (and more bad news, and more good news, and...) My contribution to #MegaFavNumbers (and my first go at YouTube, so, you know, go easy on me). Matt Parker's video, which got me thinking
From playlist MegaFavNumbers

For more cryptography, subscribe @JeffSuzukiPolymath
From playlist Elliptic Curves - Number Theory and Applications

How Shor's Algorithm Factors 314191
Go to http://www.dashlane.com/minutephysics to download Dashlane for free, and use offer code minutephysics for 10% off Dashlane Premium! Watch the main video: https://www.youtube.com/watch?v=lvTqbM5Dq4Q Support MinutePhysics on Patreon! http://www.patreon.com/minutephysics This video ex
From playlist MinutePhysics

How they found the World's Biggest Prime Number - Numberphile
Featuring Matt Parker... More links & stuff in full description below ↓↓↓ See part one at: https://youtu.be/tlpYjrbujG0 Part three on Numberphile2: https://youtu.be/jNXAMBvYe-Y Matt's interview with Curtis Cooper: https://youtu.be/q5ozBnrd5Zc The previous record: https://youtu.be/QSEKzFG
From playlist Matt Parker (standupmaths) on Numberphile
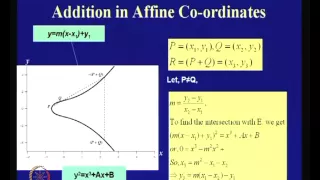
An Introduction to Elliptic Curve Cryptography
Cryptography and Network Security by Prof. D. Mukhopadhyay, Department of Computer Science and Engineering, IIT Kharagpur. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist Computer - Cryptography and Network Security

How Quantum Computers Break Encryption | Shor's Algorithm Explained
Go to http://www.dashlane.com/minutephysics to download Dashlane for free, and use offer code minutephysics for 10% off Dashlane Premium! Support MinutePhysics on Patreon! http://www.patreon.com/minutephysics This video explains Shor’s Algorithm, a way to efficiently factor large pseudop
From playlist MinutePhysics

"From Diophantus to Bitcoin: Why Are Elliptic Curves Everywhere?" by Alvaro Lozano-Robledo
This talk was organized by the Number Theory Unit of the Center for Advanced Mathematical Sciences at the American University of Beirut, on November 1st, 2022. Abstract: Elliptic curves are ubiquitous in number theory, algebraic geometry, complex analysis, cryptography, physics, and beyo
From playlist Math Talks

Alvaro Lozano-Robledo, The distribution of ranks of elliptic curves and the minimalist conjecture
VaNTAGe seminar, on Sep 29, 2020 License: CC-BY-NC-SA. An updated version of the slides that corrects a few minor issues can be found at https://math.mit.edu/~drew/vantage/LozanoRobledoSlides.pdf
From playlist Math Talks

Elliptic Curves - Lecture 6a - Ramification (continued)
This video is part of a graduate course on elliptic curves that I taught at UConn in Spring 2021. The course is an introduction to the theory of elliptic curves. More information about the course can be found at the course website: https://alozano.clas.uconn.edu/math5020-elliptic-curves/
From playlist An Introduction to the Arithmetic of Elliptic Curves

Abbey Bourdon : Minimal torsion curves in geometric isogeny classes
CONFERENCE Recording during the thematic meeting : "COUNT, COmputations and their Uses in Number Theory" the March 02, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide math
From playlist JEAN MORLET CHAIR
