
Introduction to Number Theory, Part 1: Divisibility
The first video in a series about elementary number theory, following the book by Underwood Dudley. We define the basic concept of divisibility, and prove a fundamental lemma. Intro:(0:00) Definition of Divisibility:(6:40) Our First Theorem:(9:00)
From playlist Introduction to Number Theory
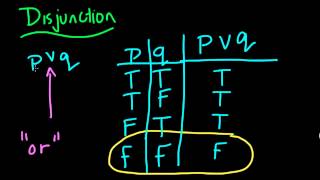
Logic - Understanding the Disjunction
a brief introduction to the idea of a disjunction in logic
From playlist Geometry

Number Theory | Divisibility Basics
We present some basics of divisibility from elementary number theory.
From playlist Divisibility and the Euclidean Algorithm

An introduction to this first course in differential equations.
From playlist Differential Equations

This math video tutorial provides a basic introduction into induction divisibility proofs. It explains how to use mathematical induction to prove if an algebraic expression is divisible by an integer. My Website: https://www.video-tutor.net Patreon Donations: https://www.patreon.com/Ma
From playlist New Precalculus Video Playlist

8b. Ch. 3, Section 3.4. Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 3, Section 3.4. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy

DIVISIBILITY - DISCRETE MATHEMATICS
We start number theory by introducing the concept of divisibility and do some simple proofs. Visit our website: http://bit.ly/1zBPlvm Subscribe on YouTube: http://bit.ly/1vWiRxW *--Playlists--* Discrete Mathematics 1: https://www.youtube.com/playlist?list=PLDDGPdw7e6Ag1EIznZ-m-qXu4XX3A0c
From playlist Discrete Math 1

10.Ch. 4, Sections 4.1-4.5. Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 4, Sections 4.1 through 4.5. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy

Natural Deductive Logic: RULES #2 (vI, vE, DN, RAA) - Logic
In this video on #Logic, we learn four more rules for natural deductive proofs. We learn disjunction introduction, disjunction elimination, double negation, and reductio ad absurdum (negation introductions, or proof by contradiction). Then we do two example proofs. #PropositionalLogic #Lo
From playlist Logic in Philosophy and Mathematics

Solve Diophantine Equation by Factoring
#shorts #mathonshorts
From playlist Elementary Number Theory

B01 An introduction to separable variables
In this first lecture I explain the concept of using the separation of variables to solve a differential equation.
From playlist Differential Equations

12. Ch. 4, Section 4.7. Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 4, Section 4.7. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy

Logic 4: Natural Deduction with Logical Axioms — Tutorial 4/4
In this four-part series we explore propositional logic, Karnaugh maps, implications and fallacies, predicate logic, existential and universal quantifiers and finally natural deduction. Become a member: https://youtube.com/Bisqwit/join My links: Twitter: https://twitter.com/RealBisqwit L
From playlist Logic Tutorial

9. Ch. 3, Sections 3.5 & 3.6. Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 3, Sections 3.5 & 3.6. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy

B22 Introduction to Substitutions
An overview of the three type of substitutions as a new method of solving linear, exact, and "almost" separable differential equations.
From playlist Differential Equations

5. Ch. 2, Sections 2.2 & 2.3. Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 2, Sections 2.2 & 2.3. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy

Logic 1: Binary Propositions, De Morgan’s Law, What is an Implication — Tutorial 1/4
In this four-part series we explore propositional logic, Karnaugh maps, implications and fallacies, predicate logic, existential and universal quantifiers and finally natural deduction. Become a member: https://youtube.com/Bisqwit/join My links: Twitter: https://twitter.com/RealBisqwit L
From playlist Logic Tutorial

3. Ch. 1 (Part 3/3). Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 1, Part 3 of 3. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy

SEM_011 - Linguistic Micro-Lectures: Disjunction (Logic)
What is disjunction (in logic) and how can the truth-value of propositions connected by logical OR and XOR be defined? Within less than two minutes Prof. Handke discusses and exemplifies the truth-conditions associated with this logical connective.
From playlist Micro-Lectures - Semantics

13. Ch. 4, Sections 4.8 & 4.9. Introduction to Logic, Philosophy 10, UC San Diego - BSLIF
Video lecture corresponding to _Basic Sentential Logic and Informal Fallacies_, Chapter 4, Sections 4.8 & 4.9. This is for the class Introduction to Logic, Philosophy 10, UC San Diego.
From playlist UC San Diego: PHIL 10 - Introduction to Logic | CosmoLearning.org Philosophy