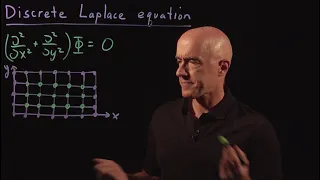Numerical differential equations
Discrete element method
A discrete element method (DEM), also called a distinct element method, is any of a family of numerical methods for computing the motion and effect of a large number of small particles. Though DEM is very closely related to molecular dynamics, the method is generally distinguished by its inclusion of rotational degrees-of-freedom as well as stateful contact and often complicated geometries (including polyhedra). With advances in computing power and numerical algorithms for nearest neighbor sorting, it has become possible to numerically simulate millions of particles on a single processor. Today DEM is becoming widely accepted as an effective method of addressing engineering problems in granular and discontinuous materials, especially in granular flows, powder mechanics, and rock mechanics. DEM has been extended into the Extended Discrete Element Method taking heat transfer, chemical reaction and coupling to CFD and FEM into account. Discrete element methods are relatively computationally intensive, which limits either the length of a simulation or the number of particles. Several DEM codes, as do molecular dynamics codes, take advantage of parallel processing capabilities (shared or distributed systems) to scale up the number of particles or length of the simulation. An alternative to treating all particles separately is to average the physics across many particles and thereby treat the material as a continuum. In the case of solid-like granular behavior as in soil mechanics, the continuum approach usually treats the material as elastic or elasto-plastic and models it with the finite element method or a mesh free method. In the case of liquid-like or gas-like granular flow, the continuum approach may treat the material as a fluid and use computational fluid dynamics. Drawbacks to homogenization of the granular scale physics, however, are well-documented and should be considered carefully before attempting to use a continuum approach. (Wikipedia).