
Topology (What is a Topology?)
What is a Topology? Here is an introduction to one of the main areas in mathematics - Topology. #topology Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, b
From playlist Topology

Topology 1.3 : Basis for a Topology
In this video, I define what a basis for a topology is. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Topology

What Is Network Topology? | Types of Network Topology | BUS, RING, STAR, TREE, MESH | Simplilearn
In this video on Network Topology, we will understand What is Network topology, the role of using topology while designing a network, Different types of Topologies in a Network. Network topology provides us with a way to configure the most optimum network design according to our requiremen
From playlist Cyber Security Playlist [2023 Updated]🔥

The Generalized Neighborhood Base Construction
The generalized neighborhood base construction of a topology is a tool for creating topological spaces some of which end up being important counterexamples in the study of general topological spaces. The construction takes its inspiration from the ability to form a base for topology from a
From playlist The CHALKboard 2022

I define closed sets, an important notion in topology and analysis. It is defined in terms of limit points, and has a priori nothing to do with open sets. Yet I show the important result that a set is closed if and only if its complement is open. More topology videos can be found on my pla
From playlist Topology

Topology 1.4 : Product Topology Introduction
In this video, I define the product topology, and introduce the general cartesian product. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Topology

Topology 1.1 : Open Sets of Reals
In this video, I give a definition of the open sets on the real numbers. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Topology

Definition of a Topological Space
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Topological Space
From playlist Topology
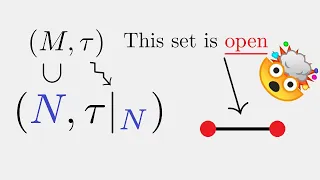
Topological Spaces: The Subspace Topology
Today, we discuss the subspace topology, which is a useful tool to construct new topologies.
From playlist Topology & Manifolds

Topological Surface States in Topological Insulators, Superconductors and Beyond - M. Zahid Hasan
DISCUSSION MEETING : ADVANCES IN GRAPHENE, MAJORANA FERMIONS, QUANTUM COMPUTATION DATES Wednesday 19 Dec, 2012 - Friday 21 Dec, 2012 VENUE Auditorium, New Physical Sciences Building, IISc Quantum computation is one of the most fundamental and important research topics today, from both th
From playlist Advances in Graphene, Majorana fermions, Quantum computation

Kathryn Hess interviewed by Peter Bubenik (August 11, 2021)
Kathryn Hess interviewed by Peter Bubenik (August 11, 2021) For more on the interview series, along with the advertisement posters, please see https://sites.google.com/view/aatrn/interviews
From playlist AATRN Interviews

John Milnor - The Abel Prize interview 2011
02:33 Beginnings, Aptitude, "socially maladjusted" 03:40 Putnam, Math. as problem-solving 04:10 First paper (at 18 yo) 06:10 John Nash, Princeton 07:45 games: Kriegspiel, Go, Nash 09:25 game theory 10:35 knot theory, Papakyriakopoulos 15:45 manifolds 17:55 dim. 7 manifolds 20:35 collaborat
From playlist The Abel Prize Interviews

Sir Michael Atiyah - The Mysteries of Space [1991]
The 64th annual Gibbs Lecture was given by Sir Michael Atiyah, Fellow of the Royal Society, of Trinity College, Cambridge, England. At a conference in San Francisco, California in January 1991, he delivered "Physics and the mysteries of space", which was filmed and made available on videot
From playlist Mathematics

Michael Atiyah: Poincaré conjecture, Hodge conjecture, Yang-Mills, Navier-Stokes [2000]
Millennium Meeting These videos document the Institute's landmark Paris millennium event which took place on May 24-25, 2000, at the Collège de France. On this occasion, CMI unveiled the "Millennium Prize Problems," seven mathematical quandaries that have long resisted solution. The announ
From playlist Number Theory

Real Topological String Amplitudes by K S Narain
11 January 2017 to 13 January 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru String theory has come a long way, from its origin in 1970's as a possible model of strong interactions, to the present day where it sheds light not only on the original problem of strong interactions, but
From playlist String Theory: Past and Present

Introduction to Homotopy Theory- PART 1: UNIVERSAL CONSTRUCTIONS
The goal of this series is to develop homotopy theory from a categorical perspective, alongside the theory of model categories. We do this with the hope of eventually developing stable homotopy theory, a personal goal a passion of mine. I'm going to follow nLab's notes, but I hope to add t
From playlist Introduction to Homotopy Theory

Topological Data Analysis and Persistent Homology -
Michael Lesnick Stanford University; Member, School of Mathematics September 28, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Adam Topaz - The Liquid Tensor Experiment - IPAM at UCLA
Recorded 13 February 2023. Adam Topaz of the University of Alberta presents "The Liquid Tensor Experiment" at IPAM's Machine Assisted Proofs Workshop. Learn more online at: http://www.ipam.ucla.edu/programs/workshops/machine-assisted-proofs/
From playlist 2023 Machine Assisted Proofs Workshop

The single, most important concept in topology and analysis: Compactness. This is explained via covers, which I'll define as well. There are tons of applications of this concept, which you can find in the playlist below Topology Playlist: https://youtube.com/playlist?list=PLJb1qAQIrmmA13v
From playlist Topology
