
Burnside's Lemma (Part 2) - combining math, science and music
Part 1 (previous video): https://youtu.be/6kfbotHL0fs Orbit-stabilizer theorem: https://youtu.be/BfgMdi0OkPU Burnside's lemma is an interesting result in group theory that helps us count things with symmetries considered, e.g. in some situations, we don't want to count things that can be
From playlist Traditional topics, explained in a new way

Burnside's Lemma (Part 1) - combining group theory and combinatorics
A result often used in math competitions, Burnside's lemma is an interesting result in group theory that helps us count things with symmetries considered, e.g. in some situations, we don't want to count things that can be transformed into one another by rotation different, like in this cas
From playlist Traditional topics, explained in a new way
Regularity lemma and its applications Part I - Fan Wei
Computer Science/Discrete Mathematics Seminar II Topic: Regularity lemma and its applications Part I Speaker: Fan Wei Affiliation: Member, School of Mathematics Dater: December 3, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Linear Algebra 2n: Spanning Sets
https://bit.ly/PavelPatreon https://lem.ma/LA - Linear Algebra on Lemma http://bit.ly/ITCYTNew - Dr. Grinfeld's Tensor Calculus textbook https://lem.ma/prep - Complete SAT Math Prep
From playlist Part 1 Linear Algebra: An In-Depth Introduction with a Focus on Applications
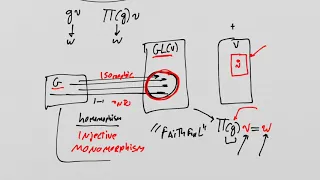
Lie Groups and Lie Algebras: Lesson 41: Elementary Representation Theory I
Lie Groups and Lie Algebras: Lesson 41: Elementary Representation Theory I I wanted to begin a more intricate example of the principle of a Universal Covering group, but I think I need to cover a little background material. We need to get a grip on what is meant by "Representation Theory"
From playlist Lie Groups and Lie Algebras

A covering of a topological space X is a topological space Y together with a continuous surjective map from X to Y that is locally bi-continuos. The infinite spiral is for example a covering of the circle. Notice how every path on the circle can be lifted to the spiral. If a coveri
From playlist Algebraic Topology

Universal covering spaces | Algebraic Topology | NJ Wildberger
We begin by giving some examples of the main theorem from the last lecture: that the associated homomorphism of fundamental groups associated to a covering space p:X to B injects pi(X) as a subgroup of pi(B). We look at helical coverings of a circle, and also a two-fold covering of the wed
From playlist Algebraic Topology
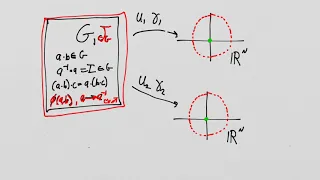
Lie Groups and Lie Algebras: Lesson 38 - Preparation for the concept of a Universal Covering Group
Lie Groups and Lie Algebras: Lesson 38 - Preparation for the Universal Covering Group concept In this lesson we examine another amazing connection between the algebraic properties of the Lie groups with topological properties. We will lay the foundation to understand how discrete invaria
From playlist Lie Groups and Lie Algebras

16. Graph limits III: compactness and applications
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX Continuing the discussion of graph limits, Prof. Zhao pro
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Manifolds 3.2 : Partitions of Unity on Normal Spaces and Imbeddings
In this video, I introduce general, topological partitions of unity, and how they can be used to imbed compact manifolds into euclidean space. Translate This Video : http://www.youtube.com/timedtext_video?ref=share&v=_6etxlOrsus Notes : None yet Patreon : https://www.patreon.com/user?u=16
From playlist Manifolds
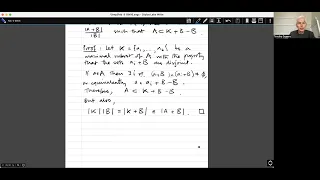
Introduction to additive combinatorics lecture 9.5 --- Freiman's theorem for subsets of F_p^N.
Freiman's theorem for subsets of F_p^N states that if A is a subset of F_p^N and |A + A| is at most C|A|, then there is a subspace X of F_p^N of size at most C'|A| that contains A, where C' depends only on C. The result is actually due to Imre Ruzsa. Here I give not Ruzsa's original proof,
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

An improved sunflower bound - Jiapeng Zhang
Computer Science/Discrete Mathematics Seminar I Topic: An improved sunflower bound Speaker: Jiapeng Zhang Affiliation: Harvard University Date: October 7, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

22. Structure of set addition II: groups of bounded exponent and modeling lemma
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX Prof. Zhao explains the Ruzsa covering lemma and uses it
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

AlgTop28: Covering spaces and fundamental groups
We illustrate the ideas from the last lectures by giving some more examples of covering spaces: of the torus, and the two-holed torus. Then we begin to explore the relationship between the fundamental groups of a covering space X and a base space B under a covering map p:X to B. For this
From playlist Algebraic Topology

Diffeomorphism Groups of Critical Regularity (Lecture 3) by Sang-hyun Kim
PROGRAM: PROBABILISTIC METHODS IN NEGATIVE CURVATURE ORGANIZERS: Riddhipratim Basu (ICTS - TIFR, India), Anish Ghosh (TIFR, Mumbai, India), Subhajit Goswami (TIFR, Mumbai, India) and Mahan M J (TIFR, Mumbai, India) DATE & TIME: 27 February 2023 to 10 March 2023 VENUE: Madhava Lecture Hall
From playlist PROBABILISTIC METHODS IN NEGATIVE CURVATURE - 2023

24. Structure of set addition IV: proof of Freiman's theorem
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX This lecture concludes the proof of Freiman's theorem on
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Vaughn Climenhaga: Closed geodesics and the measure of maximal entropy on surfaces without...
For negatively curved Riemannian manifolds, Margulis gave an asymptotic formula for the number of closed geodesics with length below a given threshold. I will describe joint work with Gerhard Knieper and Khadim War in which we obtain the corresponding result for surfaces without conjugate
From playlist Jean-Morlet Chair - Pollicott/Vaienti

Algebraic Topology - 1 - Compact Hausdorff Spaces (a Review of Point-Set Topology)
This is mostly a review point set topology. In general it is not true that a bijective continuous map is invertible (you need to worry about the inverse being continuous). In the case that your spaces are compact hausdorff this is true! We prove this in this video and review necessary fac
From playlist Algebraic Topology

Transversality and super-rigidity in Gromov-Witten Theory (Lecture - 04) by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Sites/Coverings part 2: Grothendieck Topologies
Definition of a Grothendieck topology. This is just the axiomatization of coverings.
From playlist Sites, Coverings and Grothendieck Topologies