
Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

Dihedral Group (Abstract Algebra)
The Dihedral Group is a classic finite group from abstract algebra. It is a non abelian groups (non commutative), and it is the group of symmetries of a regular polygon. This group is easy to work with computationally, and provides a great example of one connection between groups and geo
From playlist Abstract Algebra

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

Cyclic Groups (Abstract Algebra)
Cyclic groups are the building blocks of abelian groups. There are finite and infinite cyclic groups. In this video we will define cyclic groups, give a list of all cyclic groups, talk about the name “cyclic,” and see why they are so essential in abstract algebra. Be sure to subscribe s
From playlist Abstract Algebra

This is an informal talk on sporadic groups given to the Archimedeans (the Cambridge undergraduate mathematical society). It discusses the classification of finite simple groups and some of the sporadic groups, and finishes by briefly describing monstrous moonshine. For other Archimedeans
From playlist Math talks
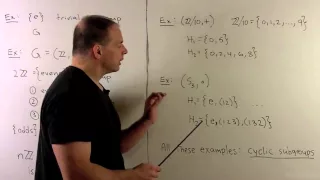
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

Abstract Algebra | The dihedral group
We present the group of symmetries of a regular n-gon, that is the dihedral group D_n. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Group Theory: The Center of a Group G is a Subgroup of G Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Theory: The Center of a Group G is a Subgroup of G Proof
From playlist Abstract Algebra

The Legendary John Conway (1937-2020) - Numberphile Podcast
We pay tribute to John Horton Conway - with clips from the man himself, plus contributions from Siobhan Roberts, David Eisenbud, Colm Mulcahy and Tony Padilla. Genius at Play by Siobhan Roberts - https://amzn.to/34ExQ4I John Conway Numberphile Playlist - https://www.youtube.com/playlist?
From playlist The Numberphile Podcast

Remembering John Conway - Part 1
Bay Area Artists and Mathematicians - BAAM! with Gathering 4 Gardner - G4G present Remembering John Conway Mathematician John Horton Conway died of COVID-19 on April 11, 2020. On April 25th, the Bay Area Artists and Mathematicians (BAAM!) hosted an informal Zoom session to share memories
From playlist Tributes & Commemorations

Allison Moore - Essential Conway spheres and Floer homology via immersed curves
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Allison Moore, Virginia Commonwealth University Title: Essential Conway spheres and Floer homology via immersed curves Abstract: We consider the problem of whether Dehn surgery along a knot in the three-sphere produces an
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021
Remembering John Conway - Part 4
Bay Area Artists and Mathematicians - BAAM! with Gathering 4 Gardner - G4G present Remembering John Conway Mathematician John Horton Conway died of COVID-19 on April 11, 2020. On April 25th, the Bay Area Artists and Mathematicians (BAAM!) hosted an informal Zoom session to share memories
From playlist Tributes & Commemorations

Remembering John Conway - Full Video
Bay Area Artists and Mathematicians - BAAM! with Gathering 4 Gardner - G4G present Remembering John Conway Mathematician John Horton Conway died of COVID-19 on April 11, 2020. On April 25th, the Bay Area Artists and Mathematicians (BAAM!) hosted an informal Zoom session to share memories
From playlist Tributes & Commemorations

This is an experimental video where I give answers to the (mostly) mathematical questions asked by viewers.
From playlist Math talks

The Genesis of Vertex Algebras
We have a guest for this very special video. Richard Borcherds (Berkeley) has contributed a video regarding the history of vertex algebras. This video was also posted on his channel and is included here as well with permission and to increase its reach. Subscribe to his channel: https:/
From playlist Vertex Operator Algebras

A Tribute to Berlekamp, Conway, Guy, Graham, and Randi - G4G14 Apr 2022
In the long four years between G4G13 and G4G14, we lost some towering figures from the G4G community. It is hard for many of us to see how we can go on without them, but their legacy will live on. In this tribute session, we honor Elwyn Berlekamp, John Conway, Richard Guy, Ron Graham, and
From playlist G4G14 Videos

This is a historical talk giving my recollections of how vertex algebras were discovered. It was requested by Michael Penn for his series of videos on vertex algebras https://www.youtube.com/playlist?list=PL22w63XsKjqyx2FFUywi_mz91Jtih52yX
From playlist Math talks

Matrix Groups (Abstract Algebra)
Matrices are a great example of infinite, nonabelian groups. Here we introduce matrix groups with an emphasis on the general linear group and special linear group. The general linear group is written as GLn(F), where F is the field used for the matrix elements. The most common examples
From playlist Abstract Algebra