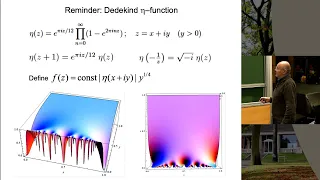
Elliptic functions | Modular forms | Fractals
In mathematics, the Dedekind eta function, named after Richard Dedekind, is a modular form of weight 1/2 and is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive. It also occurs in bosonic string theory. (Wikipedia).
Transcendental Functions 19 The Function a to the power x.mp4
The function a to the power x.
From playlist Transcendental Functions
What are the Inverse Trigonometric functions and what do they mean?
👉 Learn how to evaluate inverse trigonometric functions. The inverse trigonometric functions are used to obtain theta, the angle which yielded the trigonometric function value. It is usually helpful to use the calculator to calculate the inverse trigonometric functions, especially for non-
From playlist Evaluate Inverse Trigonometric Functions
Transcendental Functions 3 Examples using Properties of Logarithms.mov
Examples using the properties of logarithms.
From playlist Transcendental Functions
Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 1.mov
Example problems involving the integral of u to the power negative 1 du.
From playlist Transcendental Functions
Transcendental Functions 13 Derivatives of a Function and its Inverse.mov
The first derivative of a function and the inverse of that function.
From playlist Transcendental Functions
Why Do We Use the Sigmoid Function for Binary Classification?
This video explains why we use the sigmoid function in neural networks for machine learning, especially for binary classification. We consider both the practical side of making sure we get a consistent gradient from the standard categorical loss function, as well as making sure the equatio
From playlist Machine Learning
Abstract Algebra | A PID that is not a Euclidean Domain
We present an example of a principal ideal domain that is not a Euclidean domain. We follow the outline described in Dummit and Foote. In particular, we show that an integral domain D is a PID if and only if it has a Dedekind-Hasse Norm and that every Euclidean domain has a universal side
From playlist Abstract Algebra
Etale Theta - Part 02 - Properties of the Arithmetic Jacobi Theta Function
In this video we talk about Proposition 1.4 of Etale Theta. This came out of conversations with Emmanuel Lepage. Formal schemes in the Stacks Project: http://stacks.math.columbia.edu/tag/0AIL
From playlist Etale Theta
Scott Ahlgren: Algebraic and transcendental formulas for the smallest parts function
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory
Second part to this video: http://youtu.be/shEk8sz1oOw More links & stuff in full description below ↓↓↓ If the highest power of a function or polynomial is odd (e.g.: x^3 or x^5 or x^4371) then it definitely has a solution (or root) among the real numbers. Here's a nice proof demonstrate
From playlist David Eisenbud on Numberphile
Sigmoid functions for population growth and A.I.
Some elaborations on sigmoid functions. https://en.wikipedia.org/wiki/Sigmoid_function https://www.learnopencv.com/understanding-activation-functions-in-deep-learning/ If you have any questions of want to contribute to code or videos, feel free to write me a message on youtube or get my co
From playlist Analysis
Ken Ribet, Ogg's conjecture for J0(N)
VaNTAGe seminar, May 10, 2022 Licensce: CC-BY-NC-SA Links to some of the papers mentioned in the talk: Mazur: http://www.numdam.org/article/PMIHES_1977__47__33_0.pdf Ogg: https://eudml.org/doc/142069 Stein Thesis: https://wstein.org/thesis/ Stein Book: https://wstein.org/books/modform/s
From playlist Modularity and Serre's conjecture (in memory of Bas Edixhoven)
A crash course in Algebraic Number Theory
A quick proof of the Prime Ideal Theorem (algebraic analog of the Prime Number Theorem) is presented. In algebraic number theory, the prime ideal theorem is the number field generalization of the prime number theorem. It provides an asymptotic formula for counting the number of prime idea
From playlist Number Theory
Set Theory (Part 15b): Dedekind Cuts for Complicated Numbers
Please leave your questions, comments, and thoughts below! In this video, I try to give more examples of Dedekind cuts beyond the standard example of sqrt(2), such as e, pi, and sin(2). It is essential for the theory to be intelligible for there to be numerous examples. Unfortunately, not
From playlist Set Theory by Mathoma
Sergei Nechaev - Anomalous Statistics of Extreme Random Processes
I plan to discuss three problems of extremal statistics in which unusual (but related to each other) features arise: a) statistics of two-dimensional ”stretched” random walks above a semicircle, b) spectral properties of sparse random matrices, c) statistics of one-dimensional paths in
From playlist Combinatorics and Arithmetic for Physics: special days
A3 More graphs and their functions
We expand to transcendental functions such a trigonometric functions. Ply around with the Desmos calculator software and learn more about the how variables that can appear in trigonometric functions affect the graphs of those functions.
From playlist Biomathematics
Dedekind domains: Introduction
This lecture is part of an online graduate course on commutative algebra, and is an introduction to Dedekind domains. We define Dedekind domains, and give several examples of rings that are or are not Dedekind domains. This is a replacement video: as several alert viewers pointed out, t
From playlist Commutative algebra
Markus Land - L-Theory of rings via higher categories I
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics MĂĽnster: https://go.wwu
From playlist New perspectives on K- and L-theory
Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 2.mov
More example problems involving the integral of 1 over u, du.
From playlist Transcendental Functions
Set Theory (Part 14): Real Numbers as Dedekind Cuts
Please feel free to leave comments/questions on the video and practice problems below! In this video, we will construct the real number system as special subsets of rational numbers called Dedekind cuts. The trichotomy law and least upper bound property of the reals will also be proven. T
From playlist Set Theory by Mathoma