
Topology Proof The Constant Function is Continuous
Topology Proof The Constant Function is Continuous If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Topology

Proof that every Differentiable Function is Continuous
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys A proof that every differentiable function is continuous.
From playlist Calculus

Math 131 092816 Continuity; Continuity and Compactness
Review definition of limit. Definition of continuity at a point; remark about isolated points; connection with limits. Composition of continuous functions. Alternate characterization of continuous functions (topological definition). Continuity and compactness: continuous image of a com
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

Topology Proof The Composition of Continuous Functions is Continuous
Topology Proof The Composition of Continuous Functions is Continuous If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Topology

Math 131 Fall 2018 101218 Continuity and Connectedness; Discontinuities of Monotonic Functions
Recall definition of connected set. Theorem: continuous functions preserve connectedness. Proof by contraposition. Corollary: the Intermediate Value Theorem. Discontinuities on the real line: left-handed and right-handed limits. Left-continuous and right-continuous functions. Simple
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

Math 131 Fall 2018 101018 Continuity and Compactness
Definition: bounded function. Continuous image of compact set is compact. Continuous image in Euclidean space of compact set is bounded. Extreme Value Theorem. Continuous bijection on compact set has continuous inverse. Definition of uniform continuity. Continuous on compact set impl
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

This video is about continuity and some of its basic properties.
From playlist Basics: Topology
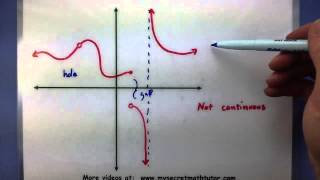
Pre-Calculus - Where is a function continuous
This video covers how you can tell if a function is continuous or not using an informal definition for continuity. Later in the video, we look at a function that is not continuous for all values, but is continuous for certain intervals. For more videos visit http://www.mysecretmathtutor.
From playlist Pre-Calculus

My submission for the Summer of Math Exposition competition: https://www.youtube.com/watch?v=ojjzXyQCzso An introduction to the idea behind the mathematical definition of continuity. If you are familiar with the epsilon-delta definition of continuity, you may recognise it here, where I
From playlist Summer of Math Exposition Youtube Videos

Daisuke Kishimoto (8/12/21): Tverberg’s theorem for cell complexes
Tverberg’s theorem states that any (d+1)(r-1)+1 points in R^d can be partitioned into r subsets whose convex hulls have a point in common. There is a topological version of it, which is often compared with an LS-version of the Borsuk-Ulam theorem. I will talk about a generalization of the
From playlist Topological Complexity Seminar

Johnathan Bush (7/8/2020): Borsuk–Ulam theorems for maps into higher-dimensional codomains
Title: Borsuk–Ulam theorems for maps into higher-dimensional codomains Abstract: I will describe Borsuk-Ulam theorems for maps of spheres into higher-dimensional codomains. Given a continuous map from a sphere to Euclidean space, we say the map is odd if it respects the standard antipodal
From playlist AATRN 2020

The Borsuk-Ulam Theorem | Nathan Dalaklis
Mappings and functions that work on topological spaces other than the real line can be counterintuitive, and in cases like with the sphere, we have things like the Borsuk-Ulam Theorem which can assert the truth of things that would appear, without proof, to be outright lies. In this video,
From playlist The First CHALKboard

Big fiber theorems and ideal-valued measures in symplectic topology - Yaniv Ganor
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Big fiber theorems and ideal-valued measures in symplectic topology Speaker: Yaniv Ganor Affiliation: Technion Date: October 22, 2021 In various areas of mathematics there exist "big fiber theorems", these a
From playlist Mathematics

The Curtis-Hedlund-Lyndon Theorem | Nathan Dalaklis | math academic talks
This is the second seminar talk that I have given as a math phd student. It is an expository academic talk that I gave as a Math PhD student during my second semester of my second year in my PhD program. The talk concerns the Factors of Symbolic Dynamical Systems and is focused on the Curt
From playlist Academic Talks

Axioms for the Lefschetz number as a lattice valuation
"Axioms for the Lefschetz number as a lattice valuation" a research talk I gave at the conference on Nielsen Theory and Related Topics in Daejeon Korea, June 28, 2013. Chris Staecker's internet webarea: http://faculty.fairfield.edu/cstaecker/ Nielsen conference webarea: http://open.nims.r
From playlist Research & conference talks

AlgTop13: More applications of winding numbers
We define the degree of a function from the circle to the circle, and use that to show that there is no retraction from the disk to the circle, the Brouwer fixed point theorem, and a Lemma of Borsuk. This is the 13th lecture of this beginner's course in Algebraic Topology, given by Assoc
From playlist Algebraic Topology: a beginner's course - N J Wildberger

From continuous rational to regulous functions – Krzysztof Kurdyka & Wojciech Kucharz – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.6 From continuous rational to regulous functions Krzysztof Kurdyka & Wojciech Kucharz Abstract: Let X be an algebraic set in ℝⁿ. Real-valued functions, defined on subsets of X, that are continuous and admit a rational representation have s
From playlist Algebraic & Complex Geometry

AlgTop14: The Ham Sandwich theorem and the continuum
In this video we give the Borsuk Ulam theorem: a continuous map from the sphere to the plane takes equal values for some pair of antipodal points. This is then used to prove the Ham Sandwich theorem (you can slice a sandwich with three parts (bread, ham, bread) with a straight planar cut
From playlist Algebraic Topology: a beginner's course - N J Wildberger

Ex 2: Find the Value of Constant to Make a Piecewise Defined Function Continuous Everywhere
This video explains how to determine the value of a constant in a one of the function rules of a piece-wise defined function in order for the function to be continuous everywhere. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com
From playlist Continuity Using Limits

Péter Nándori: Mixing and the local central limit theorem for hyperbolic dynamical systems
Abstract: We present a convenient joint generalization of mixing and the local version of the central limit theorem (MLLT) for probability preserving dynamical systems. We verify that MLLT holds for several examples of hyperbolic systems by reviewing old results for maps and presenting new
From playlist Probability and Statistics