
Alessandro Chiodo - Towards a global mirror symmetry (Part 1)
Mirror symmetry is a phenomenon which inspired fundamental progress in a wide range of disciplines in mathematics and physics in the last twenty years; we will review here a number of results going from the enumerative geometry of curves to homological algebra. These advances justify the i
From playlist École d’été 2011 - Modules de courbes et théorie de Gromov-Witten

Mirror symmetry for character varieties and field theory by Sergey Galkin
Date/Time: Wednesday, March 4, 2:00 pm Title: Mirror symmetry for character varieties and field theory Abstract: In a joint work in progress with Swarnava Mukhopadhyay and Pieter Belmans we use mirrors for projective threespaces as building blocks to construct mirrors for moduli spaces o
From playlist Seminar Series

Dimitry Gurevich - From Reflection Equation Algebra to Matrix Models
Reflection Equation Algebra is one of the Quantum matrix algebras, associated with a given Hecke symmetry, i.e. a braiding of Hecke type. I plan to explain how to introduce analogs of Hermitian Matrix Models arising from these algebras. Some other applications of the Reflection Equation Al
From playlist Combinatorics and Arithmetic for Physics: 02-03 December 2020

Homological Mirror Symmetry - Nicholas Sheridan
Nicholas Sheridan Massachusetts Institute of Technology; Member, School of Mathematics February 11, 2013 Mirror symmetry is a deep conjectural relationship between complex and symplectic geometry. It was first noticed by string theorists. Mathematicians became interested in it when string
From playlist Mathematics
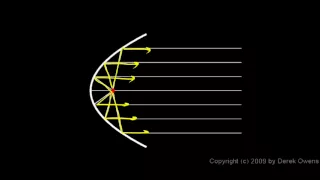
Physics 11.1.3a - Spherical and Parabolic Mirrors
Spherical and Parabolic mirrors. From the Physics course by Derek Owens. The distance learning class is available at www.derekowens.com
From playlist Physics - Reflection and Refraction

Watch more videos on http://www.brightstorm.com/math/geometry SUBSCRIBE FOR All OUR VIDEOS! https://www.youtube.com/subscription_center?add_user=brightstorm2 VISIT BRIGHTSTORM.com FOR TONS OF VIDEO TUTORIALS AND OTHER FEATURES! http://www.brightstorm.com/ LET'S CONNECT! Facebook ► https
From playlist Geometry

Alessandro Chiodo - Towards a global mirror symmetry (Part 3)
Mirror symmetry is a phenomenon which inspired fundamental progress in a wide range of disciplines in mathematics and physics in the last twenty years; we will review here a number of results going from the enumerative geometry of curves to homological algebra. These advances justify the i
From playlist École d’été 2011 - Modules de courbes et théorie de Gromov-Witten

Generalizing GKZ secondary fan using Berkovich geometry by Tony Yue Yu
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS: Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

Richard Rimanyi - Stable Envelopes, Bow Varieties, 3d Mirror Symmetry
There are many bridges connecting geometry with representation theory. A key notion in one of these connections, defined by Maulik-Okounkov, Okounkov, Aganagic-Okounkov, is the "stable envelope (class)". The stable envelope fits into the story of characteristic classes of singularities as
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Helge Ruddat: Global smoothings of toroidal crossing varieties
HYBRID EVENT Recorded during the meeting "Faces of Singularity Theory " the November 23, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovis
From playlist Mathematical Physics

Tony Yue Yu - 1/4 The Frobenius Structure Conjecture for Log Calabi-Yau Varieties
Notes: https://nextcloud.ihes.fr/index.php/s/GwJbsQ8xMW2ifb8 1/4 - Motivation and ideas from mirror symmetry, main results. --- We show that the naive counts of rational curves in an affine log Calabi-Yau variety U, containing an open algebraic torus, determine in a surprisingly simple wa
From playlist Tony Yue Yu - The Frobenius Structure Conjecture for Log Calabi-Yau Varieties

Spherical Mirrors & The Mirror Equation - Geometric Optics
This physics video tutorial provides a basic introduction into spherical mirrors such as concave mirrors and convex mirrors. It explains how to use the mirror equation to calculate the image distance given the focal length and the object distance. The focal length is the distance between
From playlist New Physics Video Playlist

Intrinsic mirror symmetry and categorical crepant resolutions - Daniel Pomerleano
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Topic: Intrinsic mirror symmetry and categorical crepant resolutions Speaker: Daniel Pomerleano Affiliation: University of Massachusetts, Boston Date: February 19, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Mirror symmetry from the SYZ base - Benjamin Gammage
Joint IAS/Princeton University Symplectic Geometry Seminar Topic: Mirror symmetry from the SYZ base Speaker: Benjamin Gammage Affiliation: Harvard University Date: October 25, 2021
From playlist Mathematics

Mirror symmetry & Looijenga's conjecture - Philip Engel
Philip Engel Columbia University October 29, 2014 A cusp singularity is an isolated surface singularity whose minimal resolution is a cycle of smooth rational curves meeting transversely. Cusp singularities come in naturally dual pairs. In the 1980's Looijenga conjectured that a cusp sing
From playlist Mathematics

First steps of non-archimedean enumerative geometry - Tony Yue Yu
Short talks by postdoctoral members Topic: First steps of non-archimedean enumerative geometry Speaker: Tony Yue Yu Affiliation: Member, School of Mathematics Date: January 30, 2017 For more video, visit http://video.ias.edu
From playlist Mathematics

http://www.teachastronomy.com/ A lot of fundamental concepts in physics are based on the idea of symmetry. Symmetry is familiar to us in an aesthetic sense. It often means things that have pleasing proportion, or look the same from every direction, or have a harmonious nature about them.
From playlist 23. The Big Bang, Inflation, and General Cosmology 2

James Propp - Conjectural Enumerations of Trimer Covers of Finite Subgraphs of the Triangular (...)
The work of Conway and Lagarias applying combinatorial group theory to packing problems suggests what we might mean by “domain-wall boundary conditions” for the trimer model on the infinite triangular lattice in which the permitted trimers are triangle trimers and three-in-a-line trimers.
From playlist Combinatorics and Arithmetic for Physics: special days

Vertex algebras, quantum master equation and mirror symmetry - Si Li
Workshop on Homological Mirror Symmetry: Emerging Developments and Applications Topic: Vertex algebras, quantum master equation and mirror symmetry Speaker: Si Li Affiliation: Tsinghua University Date: March 15, 2017 For more video, visit http://video.ias.edu
From playlist Mathematics

Variation of FLTZ skeleta - Jesse Huang
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Topic: Variation of FLTZ skeleta Speaker: Jesse Huang Affiliation: UIUC Date: March 26, 2021 Speaker's corrections: 1) The linear map on page 10 should be sending the basis to 1 and -1, not 1 and 2; 2) one more typo on the
From playlist Mathematics