Convex analysis | Convex geometry | Linear programming
Dual cone and polar cone
Dual cone and polar cone are closely related concepts in convex analysis, a branch of mathematics. (Wikipedia).
Convex analysis | Convex geometry | Linear programming
Dual cone and polar cone are closely related concepts in convex analysis, a branch of mathematics. (Wikipedia).
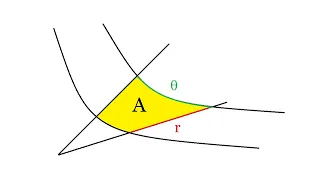
In this video, I introduce the hyperbolic coordinates, which is a variant of polar coordinates that is particularly useful for dealing with hyperbolas (and 3 dimensional versions like hyperboloids of one sheet or two sheets). Suprisingly (or not), they involve the hyperbolic trig functions
From playlist Double and Triple Integrals
From playlist GeoGebra 3D

This is a follow-up of the integral of exp(-x^2) video on blackpenredpen's channel, in case you're wondering how to get that extra factor of r in the integral. It's mathemagical! :D Here's the like to the original video: Gaussian Integral https://youtu.be/r9W8YWELXvg
From playlist Double and Triple Integrals

"AWESOME Antigravity double cone" (science experiments)
Physics (la physique). Explain why double cone goes up on inclaned plane (science experiments)
From playlist MECHANICS
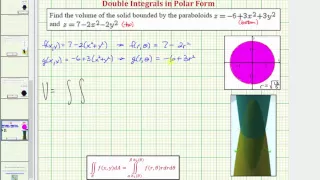
Double Integrals in Polar Form - Volume Bounded by Two Paraboloids
This video explains how to use a double integral in polar form to determine the volume bounded to two paraboloids. http://mathispower4u.com
From playlist Double Integrals in Polar Coordinates
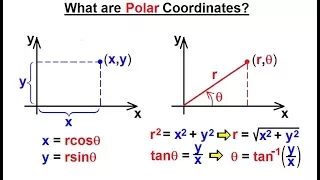
Calculus 2: Polar Coordinates (1 of 38) What are Polar Coordinates?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what are polar coordinates and Cartesian coordinates. The Cartesian coordinates use x and y to locate a point on a plane, and the polar coordinates use r and theta to locate a point on a plane
From playlist THE "WHAT IS" PLAYLIST

Extending the Prym map - Samuel Grushevsky
Samuel Grushevsky Stony Brook University February 10, 2015 The Torelli map associates to a genus g curve its Jacobian - a gg-dimensional principally polarized abelian variety. It turns out, by the works of Mumford and Namikawa in the 1970s (resp. Alexeev and Brunyate in 2010s), that the T
From playlist Mathematics

Spectrahedral lifts of convex sets – Rekha Thomas – ICM2018
Control Theory and Optimization Invited Lecture 16.6 Spectrahedral lifts of convex sets Rekha Thomas Abstract: Efficient representations of convex sets are of crucial importance for many algorithms that work with them. It is well-known that sometimes, a complicated convex set can be expr
From playlist Control Theory and Optimization

Perpendicularity, polarity and duality on a sphere | Universal Hyperbolic Geometry 37
This video discusses perpendicularity on a sphere, associating two poles to every great circle, and one polar line (great circle) to every point. This association is cleaner in elliptic geometry, where there is then a 1-1 correspondence between elliptic points (pairs of antipodal points on
From playlist Universal Hyperbolic Geometry

Inaugural Imaging & Inverse Problems (IMAGINE) OneWorld SIAM-IS Virtual Seminar Series Talk
Date: Wednesday, October 14, 10:00am EDT Speaker: Michael Friedlander, University of British Columbia Title: Polar deconvolution of mixed signals Abstract: The signal demixing problem seeks to separate the superposition of multiple signals into its constituent components. We model the s
From playlist Imaging & Inverse Problems (IMAGINE) OneWorld SIAM-IS Virtual Seminar Series

Factorization through L2, Rounding and Duality Part 2 - Vijay Bhattiprolu
Computer Science/Discrete Mathematics Seminar II Topic: Factorization through L2, Rounding and Duality Part 2 Speaker: Vijay Bhattiprolu Affiliation: Member, School of Mathematics Date: November 24, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

The Three/Four bridge and Apollonius duality for conics | Six: A course in pure maths 5 | Wild Egg
The Three / Four bridge plays an important role in understanding the remarkable duality discover by Apollonius between points and lines in the plane once a conic is specified. This is a purely projective construction that works for ellipses, and their special case of a circle, for parabola
From playlist Six: An elementary course in Pure Mathematics
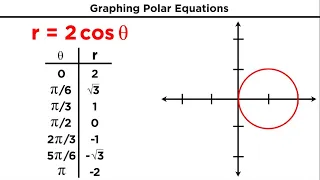
Polar Coordinates and Graphing Polar Equations
Everything we have done on the coordinate plane so far has been using rectangular coordinates. That's the x and y we are used to. But that's not the only coordinate system. We can also use polar coordinates, which graph points in terms of a radius, or distance from a pole, and theta, the a
From playlist Mathematics (All Of It)

Stanislaw Szarek: The projective/injective ratio and GPTs
Among natural tensor products of normed spaces, the projective and the injective are the extreme ones. The question : How much do they differ? was considered by Grothendieck and Pisier (in the 1950s and 1980s), but - surprisingly - no systematic quantitative analysis of the finite- dimensi
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects

Mirror symmetry from the SYZ base - Benjamin Gammage
Joint IAS/Princeton University Symplectic Geometry Seminar Topic: Mirror symmetry from the SYZ base Speaker: Benjamin Gammage Affiliation: Harvard University Date: October 25, 2021
From playlist Mathematics

Introduction to Double Integrals in Polar Coordinates
This video introduces double integrals in polar form and provides two examples of converting a double integral given in rectangular form to polar form. http://mathispower4u.wordpress.com/
From playlist Double Integrals in Polar Coordinates
https://www.math.ias.edu/files/media/agenda.pdf More videos on http://video.ias.edu
From playlist Mathematics

Double Integrals in Polar Coordinates - Example 2
This is a second example of how to rewrite a double integral given in rectangular form in polar form. http://mathispower4u.wordpress.com/
From playlist Double Integrals in Polar Coordinates

Automorphic Cohomology II (Carayol's work and an Application) - Phillip Griffiths
Phillip Griffiths Professor Emeritus, School of Mathematics April 6, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics