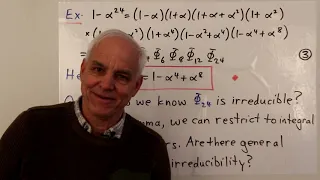
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Irreducibility (Eisenstein's Irreducibility Criterion)
Given a polynomial with integer coefficients, we can determine whether it's irreducible over the rationals using Eisenstein's Irreducibility Criterion. Unlike some our other technique, this works for polynomials of high degree! The tradeoff is that it works over the rationals, but need not
From playlist Modern Algebra - Chapter 11

From playlist Courses and Series

The Routh-Hurwitz Stability Criterion
In this video we explore the Routh Hurwitz Stability Criterion and investigate how it can be applied to control systems engineering. The Routh Hurwitz Stability Criterion can be used to determine how many roots of a polynomial are in the right half plane. Topics and time stamps: 0:00 –
From playlist Control Theory

RNT2.6.2. Eisenstein's Criterion
Ring Theory: Continuing with Gauss' Lemma, we prove Eisenstein's Criterion for Irreducibility and that R UFD implies R[x] UFD. As an example of EC, we show that f(x) = x^4+x^3+x^2+x+1 is irreducible over the integers using substitution.
From playlist Abstract Algebra

This educational video delves into how you quantify a linear statistical relationship between two variables using covariance! #statistics #probability #SoME2 This video gives a visual and intuitive introduction to the covariance, one of the ways we measure a linear statistical relation
From playlist Summer of Math Exposition 2 videos

Voting Theory: Fairness Criterion
This video define 4 Fairness Criterion for determining the winner of an election. Site: http://mathispower4u.com
From playlist Voting Theory

Covariance (1 of 17) What is Covariance? in Relation to Variance and Correlation
Visit http://ilectureonline.com for more math and science lectures! To donate:a http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn the difference between the variance and the covariance. A variance (s^2) is a measure of how spread out the numbers of
From playlist COVARIANCE AND VARIANCE

Rings 16 Factorization of polynomials
This lecture is part of an online course on rings and modules. We discuss the problem of factorising polynomials with integer coefficients, and in particular give some tests to see whether they are irreducible. For the other lectures in the course see https://www.youtube.com/playlist?lis
From playlist Rings and modules

In this video I discuss irreducible polynomials and tests for irreducibility. Note that this video is intended for students in abstract algebra and is not appropriate for high-school or early college level algebra courses.
From playlist Abstract Algebra

Proving a Polynomial is Irreducible with Eisentein's Criterion
Proving a Polynomial is Irreducible with Eisentein's Criterion If you enjoyed this video please consider liking, sharing, and subscribing. Udemy Courses Via My Website: https://mathsorcerer.com My FaceBook Page: https://www.facebook.com/themathsorcerer There are several ways that you c
From playlist Abstract Algebra

Abstract Algebra | Eisenstein's criterion
We present a proof of Eisenstein's criterion along with some examples. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.michael-penn.net Randolph College Math: http://www.randolphcollege.edu/mathematics/ Research Gate profile: htt
From playlist Abstract Algebra

A Tameness Criterion for Generic Modular Mod p Galois Representations by Daniel Le
PROGRAM STATISTICAL BIOLOGICAL PHYSICS: FROM SINGLE MOLECULE TO CELL (ONLINE) ORGANIZERS Debashish Chowdhury (IIT Kanpur), Ambarish Kunwar (IIT Bombay) and Prabal K Maiti (IISc, Bengaluru) DATE & TIME 07 December 2020 to 18 December 2020 VENUE Online 'Fluctuation-and-noise' are themes tha
From playlist Recent Developments Around P-adic Modular Forms (Online)

Bunchwise Balance and Irreducible Sequences in the Light-Heavy... by Kabir Ramola (TIFR,Hyderabad)
DISCUSSION MEETING STATISTICAL PHYSICS: RECENT ADVANCES AND FUTURE DIRECTIONS (ONLINE) ORGANIZERS: Sakuntala Chatterjee (SNBNCBS, Kolkata), Kavita Jain (JNCASR, Bangalore) and Tridib Sadhu (TIFR, Mumbai) DATE: 14 February 2022 to 15 February 2022 VENUE: Online In the past few dec
From playlist Statistical Physics: Recent advances and Future directions (ONLINE) 2022

Trigonometry 7 The Cosine of the Sum and Difference of Two Angles
A geometric proof of the cosine of the sum and difference of two angles identity.
From playlist Trigonometry


