
James Stasheff (8/31/22): Homotopy coherence - theme and variations
This survey will be semi-historical and idiosyncratic with the topics covered determined by the knowledge and taste of the authors, but we hope it will provide some links that may not be common knowledge between the various aspects of the theory of homotopy coherence and, in particular, to
From playlist AATRN 2022

Introduction to Homotopy Theory- PART 1: UNIVERSAL CONSTRUCTIONS
The goal of this series is to develop homotopy theory from a categorical perspective, alongside the theory of model categories. We do this with the hope of eventually developing stable homotopy theory, a personal goal a passion of mine. I'm going to follow nLab's notes, but I hope to add t
From playlist Introduction to Homotopy Theory
Cohomology in Homotopy Type Theory - Eric Finster
Eric Finster Ecole Polytechnique Federal de Lausanne; Member, School of Mathematics March 6, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

Homotopy type theory: working invariantly in homotopy theory -Guillaume Brunerie
Short talks by postdoctoral members Topic: Homotopy type theory: working invariantly in homotopy theory Speaker: Guillaume Brunerie Affiliation: Member, School of Mathematics Date: September 26, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Homomorphisms in abstract algebra
In this video we add some more definition to our toolbox before we go any further in our study into group theory and abstract algebra. The definition at hand is the homomorphism. A homomorphism is a function that maps the elements for one group to another whilst maintaining their structu
From playlist Abstract algebra
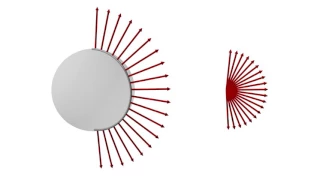
Homotopy elements in the homotopy group π₂(S²) ≅ ℤ. Roman Gassmann and Tabea Méndez suggested some improvements to my original ideas.
From playlist Algebraic Topology

Introduction to Homotopy Theory- Part 5- Transition to Abstract Homotopy Theory
Credits: nLab: https://ncatlab.org/nlab/show/Introdu... Animation library: https://github.com/3b1b/manim Music: ► Artist Attribution • Music By: "KaizanBlu" • Track Name: "Remember (Extended Mix)" • YouTube Track Link: https://bit.ly/31Ma5s0 • Spotify Track Link: https://spoti.fi/
From playlist Introduction to Homotopy Theory

Homotopy Group - (1)Dan Licata, (2)Guillaume Brunerie, (3)Peter Lumsdaine
(1)Carnegie Mellon Univ.; Member, School of Math, (2)School of Math., IAS, (3)Dalhousie Univ.; Member, School of Math April 11, 2013 In this general survey talk, we will describe an approach to doing homotopy theory within Univalent Foundations. Whereas classical homotopy theory may be des
From playlist Mathematics

Stable Homotopy Seminar, 14: The stable infinity-category of spectra
I give a brief introduction to infinity-categories, including their models as simplicially enriched categories and as quasi-categories, and some categorical constructions that also make sense for infinity-categories. I then describe what it means for an infinity-category to be stable and h
From playlist Stable Homotopy Seminar

Homotopy Category As a Localization by Rekha Santhanam
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Cohomology in difference algebra and geometry We view difference algebra as the study of algebraic objects in the topos of difference sets, i.e., as `ordinary algebra’ in a new universe. The methods of topos theory and categorical logic enable us to develop difference homological algebra,
From playlist DART X

Emily Riehl: On the ∞-topos semantics of homotopy type theory: All ∞-toposes have... - Lecture 3
HYBRID EVENT Recorded during the meeting "Logic and Interactions" the February 24, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual M
From playlist Topology

Yonatan Harpaz - New perspectives in hermitian K-theory I
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Stable Homotopy Seminar, 9: Infinite Loop Spaces, and Homotopy Colimits
The fibrant spectra are the Ω-spectra, and we can give an elegant explicit description of the fibrant replacement. The "infinite loop space" functor, which is the derived right adjoint to the suspension spectrum, is then given by taking the 0th space of an equivalent Ω-spectrum. This allow
From playlist Stable Homotopy Seminar

Stable Homotopy Seminar, 1: Introduction and Motivation
We describe some features that the category of spectra is expected to have, and some ideas from topology it's expected to generalize. Along the way, we review the Freudenthal suspension theorem, and the definition of a generalized cohomology theory. ~~~~~~~~~~~~~~~~======================
From playlist Stable Homotopy Seminar

Ben Antieau: Negative and homotopy K-theoretic extensions of the theorem of the heart
The lecture was held within the framework of the Hausdorff Trimester Program : Workshop "K-theory in algebraic geometry and number theory"
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Angélica M. Osorno - Equivariant Infinite Loop Space Machines
An equivariant infinite loop space machine is a functor that constructs genuine equivariant spectra out of simpler categorical or space level data. In the late 80’s Lewis–May–Steinberger and Shimakawa developed generalizations of the operadic approach and the G-space approach respectively.
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Simplicial Types - Peter Lumsdaine
Peter Lumsdaine Dalhousie University; Member, School of Mathematics January 16, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

In this first video on cosets, I show you the equivalence relation on a group, G, that will turn out to create equivalence classes, which are actually cosets. We will prove later that these equivalence classes created by an element in the group, G, are equal to the set of element made up
From playlist Abstract algebra