
Here is a wonderful theorem about the intersection of decreasing closed sets, called the Cantor Intersection Theorem, also known as the Finite Intersection Property. Enjoy! Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHGGBXRMV32EKVI Subscribe to my channel:
From playlist Topology

In this video, I discuss the finite intersection property, which is a nice generalization of the Cantor Intersection Theorem and a very elegant application of compactness. Enjoy this topology-filled adventure! Compactness: https://youtu.be/xiWizwjpt8o Cantor Intersection Theorem: https:/
From playlist Topology

What is an Intersection? (Set Theory)
What is the intersection of sets? This is another video on set theory in which we discuss the intersection of a set and another set, using the classic example of A intersect B. We do not quite go over a formal definition of intersection of a set in this video, but we come very close! Be su
From playlist Set Theory

Cantor's theorem, formally proven
In this video we're going to give an explicit proof of Cantor's theorem and also go a little deeper in understanding the offending set in the famous diagonal construction employed here. https://en.wikipedia.org/wiki/Cantor%27s_theorem https://en.wikipedia.org/wiki/Cantor%27s_diagonal_argu
From playlist Logic

Maths for Programmers: Sets (DeMorgan’s Law (Examples))
We're busy people who learn to code, then practice by building projects for nonprofits. Learn Full-stack JavaScript, build a portfolio, and get great references with our open source community. Join our community at https://freecodecamp.com Follow us on twitter: https://twitter.com/freecod
From playlist Maths for Programmers
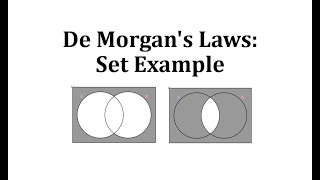
This lesson provides a set example of De Morgan's Laws.
From playlist Sets (Discrete Math)

Counting formula for two intersecting sets: N(A union B)=N(A)+N(B)-N(A intersect B)
Previously we saw a sample space is a disjoint union and we had a summation rule to count probabilities in this scenario. Now we consider a non-disjoint union where there is a nontrivial intersection between the two sets. The formula for the number of elements in the union of A and B is th
From playlist Discrete Math (Full Course: Sets, Logic, Proofs, Probability, Graph Theory, etc)

The Cantor Set, one of the most important sets in mathematics. Come and see why it’s so important, enjoy! Cantor Intersection Theorem https://youtu.be/PybSLopesaE Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHGGBXRMV32EKVI Subscribe to my channel: youtube.c
From playlist Topology

Dynamical systems, fractals and diophantine approximations – Carlos Gustavo Moreira – ICM2018
Plenary Lecture 6 Dynamical systems, fractal geometry and diophantine approximations Carlos Gustavo Moreira Abstract: We describe in this survey several results relating Fractal Geometry, Dynamical Systems and Diophantine Approximations, including a description of recent results related
From playlist Plenary Lectures
A. Wright - Mirzakhani's work on Earthquakes (Part 1)
We will give the proof of Mirzakhani's theorem that the earthquake flow and Teichmuller unipotent flow are measurably isomorphic. We will assume some familiarity with quadratic differentials, but no familiarity with earthquakes, and the first lecture will be devoted to preliminaries. The s
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

Real Analysis Ep 6: Countable vs uncountable
Episode 6 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class. This episode is about countable and uncountable sets, Cantor's theorem, and the continuum hypothesis. Class webpage: http://cstaecker.fairfield.edu/~cstaecker/c
From playlist Math 3371 (Real analysis) Fall 2020

Ex: Determine Cardinality of the Intersection of Two Sets Using a Venn Diagram
This video explains how to create a Venn Diagram to determine the number of elements in the intersection of sets. Site: http://mathispower4u.com
From playlist Sets

On Zaremba's Conjecture - Alex Kontorovich
Alex Kontorovich Stony Brook University April 22, 2011 Inspired by the theory of good lattice points in numerical integration, Zaremba conjectured in 1972 that for every denominator q, there is some coprime numerator p, such that the continued fraction expansion of p/q has uniformly bounde
From playlist Mathematics

Ahlfors-Bers 2014 "Roots of Polynomials and Parameter Spaces"
Sarah Koch (University of Michigan): In his last paper, "Entropy in Dimension One," W. Thurston completely characterized which algebraic integers arise as exp(entropy(f)), where f is a postcritically finite real map of a closed interval. On page 1 of this paper, there is a spectacular ima
From playlist The Ahlfors-Bers Colloquium 2014 at Yale

Danny Calegari: Big Mapping Class Groups - lecture 1
Part I - Theory : In the "theory" part of this mini-course, we will present recent objects and phenomena related to the study of big mapping class groups. In particular, we will define two faithful actions of some big mapping class groups. The first is an action by isometries on a Gromov-h
From playlist Topology

Semiclassical analysis, chaotic dynamics, and fractal uncertainty principle - Semyon Dyatlov
Emerging Topics Working Group Topic: Semiclassical analysis, chaotic dynamics, and fractal uncertainty principle Speaker: Semyon Dyatlov Affiliation: Massachusetts Institute of Technology Date: October 10, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

A Useful Lemma about Intersections of Sets and Some Applications - Vitaly Bergelson
Special Year Learning Seminar [REC DO NOT PUBLISH] 10:30am|Simonyi 101 and Remote Access Topic: A Useful Lemma about Intersections of Sets and Some Applications Speaker: Vitaly Bergelson Affiliation: Ohio State University; Member, School of Mathematics Date: February 8 2023 The "interse
From playlist Mathematics

Smoothing finite group actions on three-manifolds – John Pardon – ICM2018
Topology Invited Lecture 6.13 Smoothing finite group actions on three-manifolds John Pardon Abstract: There exist continuous finite group actions on three-manifolds which are not smoothable, in the sense that they are not smooth with respect to any smooth structure. For example, Bing co
From playlist Topology