
Fluid flow for cos(x+y)i + sin(xy)j
From playlist Curl

How to increase tap water flow
Recently I noticed my bathroom tap water flow is very small. This is a small tweak on how to increase it. Enjoy.
From playlist Everyday How-to

Daniel Tataru: Geometric heat flows and caloric gauges
Abstract: Choosing favourable gauges is a crucial step in the study of nonlinear geometric dispersive equations. A very successful tool, that has emerged originally in work of Tao on wave maps, is the use of caloric gauges, defined via the corresponding geometric heat flows. The aim of thi
From playlist Mathematical Physics
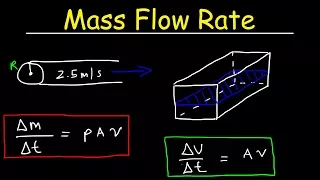
Volume Flow Rate & Mass Flow Rate - Fluid Dynamics Physics Problems
This physics video tutorial provides a basic introduction into mass flow rate and volume flow rate. The mass flow rate is the change in mass per unit time. It is also equal to the product of the fluid density, cross sectional area and the speed of the fluid in a pipe. The volume flow ra
From playlist New Physics Video Playlist

Physics - Fluid Dynamics (1 of 25) Viscosity & Fluid Flow: Introduction
Visit http://ilectureonline.com for more math and science lectures! In this video I will introduce viscosity and fluid flow involving frictional forces between the molecules and the containing walls. Next video in this series can be seen at: https://youtu.be/3xukKynwA70
From playlist PHYSICS 34 FLUID DYNAMICS

Alexander Belavin - Spectral Flow Construction of N=2 Superconformal Orbifolds
Ten-dimensional Superstring theory unifies the Standard Model and quantum gravity. To obtain a four-dimensional theory with Space-Time Supersymmetry (which is necessary for phenomenological reasons), as shown by Candelas, Horowitz, Strominger, Witten, we must compactify six of the ten dime
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Physics: Fluid Dynamics: Bernoulli's & Flow in Pipes (1 of 38) Parameters Affecting Flow
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain fluid dynamics in an imperfect world where the fluid flow in pipes are affected by: 1) increase in length increases the friction force; 2) increase in roughness increases frictional losses; 3)
From playlist PHYSICS 34.1 BERNOULLI'S EQUATION & FLOW IN PIPES

Holomorphic Cartan geometries on simply connected manifolds by Sorin Dumitrescu
Discussion Meeting Complex Algebraic Geometry ORGANIZERS: Indranil Biswas, Mahan Mj and A. J. Parameswaran DATE:01 October 2018 to 06 October 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore The discussion meeting on Complex Algebraic Geometry will be centered around the "Infosys-ICT
From playlist Complex Algebraic Geometry 2018

Student Video: Fluid Flow in Pipes and Rivers
MIT RES.3-004 Visualizing Materials Science, Fall 2017 Speaker: Sarith Bandara View the complete course: https://ocw.mit.edu/RES-3-004F17 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62EJXwSgoVRfh1tEiSc01bh Describes how fluids flow in pipes and rivers. License: Cre
From playlist MIT RES.3-004 Visualizing Materials Science, Fall 2017

Wrapped Floer theory and Homological mirror symmetry for toric Calabi-Yau manifolds - Yoel Groman
Princeton/IAS Symplectic Geometry Seminar Topic: Wrapped Floer theory and Homological mirror symmetry for toric Calabi-Yau manifolds Speaker: Yoel Groman Affiliation: Columbia University Date: October 9, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Heather Macbeth: Kähler-Ricci solitons on crepant resolutions of finite quotients of C^n
Abstract: By a gluing construction, we produce steady Kähler-Ricci solitons on equivariant crepant resolutions of ℂ^n/GCn/G, where GG is a finite subgroup of SU(n)SU(n), generalizing Cao’s construction of such a soliton on a resolution of ℂ^n/ℤnCn/Zn. This is joint work with Olivier Biquar
From playlist Algebraic and Complex Geometry

Metrics of constant Chern scalar curvature and a Chern-Calabi flow
Speaker: Sisi Shen (Northwestern) Abstract: We discuss the existence problem of constant Chern scalar curvature metrics on a compact complex manifold. We prove a priori estimates for these metrics conditional on an upper bound on the entropy, extending a recent result by Chen-Cheng in the
From playlist Informal Geometric Analysis Seminar

Denis Auroux - Towards homological mirror symmetry for affine varieties
Denis AUROUX (U.C. Berkeley, USA)
From playlist Algèbre, Géométrie et Physique : une conférence en l'honneur

Orbifolds and Systolic Inequalities - Christian Lange
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Orbifolds and Systolic Inequalities Speaker: Christian Lange Affiliation: Mathematisches Institut der Universität München Date: January 13, 2023 In this talk, I will first discuss some instances in which orbi
From playlist Mathematics

Tony Yue Yu - 2/4 The Frobenius Structure Conjecture for Log Calabi-Yau Varieties
Notes: https://nextcloud.ihes.fr/index.php/s/8KTr2Mfdk22rpqX 2/4 - Skeletal curves: a key notion in the theory. --- We show that the naive counts of rational curves in an affine log Calabi-Yau variety U, containing an open algebraic torus, determine in a surprisingly simple way, a family
From playlist Tony Yue Yu - The Frobenius Structure Conjecture for Log Calabi-Yau Varieties
Johannes Nicaise: The non-archimedean SYZ fibration and Igusa zeta functions - part 3/3
Abstract : The SYZ fibration is a conjectural geometric explanation for the phenomenon of mirror symmetry for maximal degenerations of complex Calabi-Yau varieties. I will explain Kontsevich and Soibelman's construction of the SYZ fibration in the world of non-archimedean geometry, and its
From playlist Algebraic and Complex Geometry

Fluid flow with four points of curl interest
From playlist Curl

SUSY for Strings and Branes, Part 3 - Melanie Becker
SUSY for Strings and Branes, Part 3 Melanie Becker Texas A&M University July 22, 2010
From playlist PiTP 2010

